截断误差、舍入误差与科学计算中的陷阱¶
庞龙刚 @ 华中师范大学
学习目标¶
认识截断误差(Truncation Error)、舍入误差(Rounding Error)
认识使用计算机做数值计算可能遇到的陷阱
主动规避,快速定位,解决遇到的陷阱
学习任务¶
- 截断误差
- 熟悉 float32,float64(double),舍入误差
- 知道一个数据类型能表示的最大,最小数,防止溢出
- 避免大数加小数,或对大量浮点数的连加操作
- 避免两个相近的数相减
- 避免对浮点数使用“相等”比较
- 熟悉 NaN (Not A Number), inf
- 预估任务复杂度、内存和硬盘占用
截断误差:从口算开根号说起¶
有一个神奇的公式,根据它可以口算常见正整数的根号。这个公式就是,
\begin{align} \sqrt{n+\Delta n} \approx \sqrt{n} + \frac{\Delta n}{2 \sqrt{n}} \end{align}比如,对于 $\sqrt{26}$, 上面式子中 $n=25$, $\Delta n=1$, 口算得到 $\sqrt{26} \approx 5 + \frac{1}{2\times 5} = 5.1$ 。使用计算器得到的 $\sqrt{26}=5.099019...$, 上面的口算结果非常接近正确值。
上面的式子对于 $n=1, 4, 9, 16, 25, 36, ..., 81$ 等等都很好计算,
- $\sqrt{10} = 3.16227 \approx 3 + \frac{10 - 9}{2\times 3} = 3.1667$,
- $\sqrt{82} \approx 9 + \frac{1}{2 \times 9} = 9\frac{1}{18}$
这个公式来自哪里呢?它来自于泰勒展开公式。 $$ f(x+ \Delta x) = f(x) + f'(x)\Delta x + \frac{1}{2!}f''(x)\Delta x^2 + \cdots $$ 将 $\sqrt{x+\Delta x}$ 泰勒展开, $$ \sqrt{x+ \Delta x} = \sqrt{x} + \frac{\Delta x}{2\sqrt{x}} - \frac{1}{8} \frac{\Delta x^2}{(\sqrt{x})^3} + \cdots $$ 可以看到,口算开根号公式是泰勒展开的前两项。
这个公式的后面所有高阶项都被省略,称为截断误差 $O(- \frac{1}{8} \frac{\Delta x^2}{(\sqrt{x})^3} + \cdots)$。
可以尝试口算 $\sqrt{99} = 9 + \frac{18}{2\times 9} = 10$, 计算器算出来的值为 9.94987。因为 $\Delta x$ 与 $\sqrt{x}$ 的比值较大,此时截断误差的首项为
$- \frac{1}{8} \frac{\Delta x^2}{(\sqrt{x})^3} = - \frac{1}{8} \frac{18^2}{(9)^3} = - \frac{1}{18} \approx -0.05$
知道了泰勒展开公式,就可以将上面的口算开根号公式推广, $$ \sqrt{n-\Delta n} \approx \sqrt{n} - \frac{\Delta n}{2 \sqrt{n}} $$ 从离 99 更近的 100 开始计算,则 $\sqrt{99} =\sqrt{100-1} \approx 10 - \frac{1}{2\times 10} = 9.95$, 更加接近真实值 9.94987。
习题 1:使用泰勒展开公式笔算 $\cos(31^{\circ})$,并估计截断误差。
习题 2:使用泰勒展开公式说明,为何谐振子势 $V(x) = \frac{1}{2} x^2$ 在物理中应用如此广泛。(提示:束缚态势函数 V(x) 在极小值附近展开)
浮点数与舍入误差¶
理论上实数可以有无穷多位,比如圆周率 $\pi$,
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 .....
计算机只能用有限个 bit 表示实数, 引入了舍入误差,
根据 IEEE754 标准,使用 32 和 64 个二进制的 bit 表示的浮点数分别被称为单精度和双精度浮点数,它们是科学计算中最常用的数据类型,
- float32 (single precision),有效数字约为 7 位, $\pi = 3.1415927$
- float64 (double precision),有效数字约为 16 位, $\pi= 3.141592653589793$
import numpy as np
print("float32(pi)=", np.float32(np.pi))
print("float64(pi)=", np.float64(np.pi))
单精度浮点数 (float32),使用
- 1 个 bit 表示正负号,记为 s
- 23 个 bit 表示有效数字,记为 $a_0 a_1 \cdots a_{23}$
- 8 个 bit 表示指数位,记为 $b_0 b_1 \cdots b_7$
每个 bit 只有 0 或 1 两个取值。整个浮点数记为,
\begin{align} x = (-1)^s \times a \times 2^{b - E} \end{align}其中 E 表示最大指数位的一半,E(float32) = 127 = $2^7 = 1111111_2$。
# 科学计数法
x = 1.0E-10 # 表示 1乘10的-10次方,对应内部二进制表示 ( s=0, a=0000...001, b-E<0)
y = -1.0E8 # 对应内部二进制表示 ( s=1, a=0000...001, b-E>0)
最大的浮点数与数值溢出¶
如果 x 是最大的浮点数,则 2x 会出现数值溢出
# python 默认的 float 为 float64(double)类型,
import sys
sys.float_info
x = sys.float_info.max
print("x=", x)
print("(2*x)/5=", (2 * x) / 5)
print("0.4*x=", 0.4*x)
# numpy 的 float32 类型可以表示的最大数
x = np.finfo(np.float32).max
print('x=', x)
print('2 x=', np.float32(2 * x))
np.finfo(np.float32)
float32: 4 个字节 (Bytes),每个字节8个比特(bit),总共 32 个比特,每个比特取值 0 或 1
float32 负数表示范围:-3.4028235E+38 到 -1.401298E-45
float32 正数表示范围:1.401298E-45 到 3.4028235E+38
因为小数点后有效数字只有6位,float32 没有能力完整表示 100 + 10E-6
大数加小数遇到的困难¶
float32 精度下,下面这两个数相加,结果是多少?
A = 3.1415927
B = 0.00000005
如果 B 的值小于 A 的舍入误差,则 A+B 的计算与B无关。
# 小数被吃掉
np.float32(np.pi) + np.float32(5E-8)
A = np.float32(1.0E2)
B = np.float32(1.0E-6)
A + B
举例:夸克胶子等离子体冷却超曲面上发射出的强子数计算使用 Cooper-Frye 公式,
\begin{align} \int p_{\mu} d\Sigma^{\mu} f(p, T) = \sum_i p_{\mu} d\Sigma^{\mu}_i f(p, T) \end{align}其中 $f(p\cdot u, T) = (2s+1)/(e^{p\cdot u / T} \pm 1)$ 是费米子(+)或玻色子(-)满足的分布函数。
计算中将整个球面分割成几百万个小多边形,计算流过这些多边形的粒子数, 最后对几百万个小片求和。
在将代码从 CPU (float64)到 GPU (float32) 上移植时,发现累积误差可以大到 $5\%$!
# 大数加小数困难示例:小数连加
from tqdm import tqdm
loops = int(1E7)
res = np.float32(0.0)
dx = np.float32(1.0E-7)
for i in tqdm(range(loops)):
res += dx
# 真实结果
ground_truth = loops*dx
print("theoretical results: %s"%(ground_truth))
print("accumulated sum:", res)
print("relative error = ", (res-ground_truth)/ground_truth)
在 c/c++ 语言中, float32 记为 float,float64 记为 double。
python 中默认 float 为 float64
numpy:np.float32 或 np.float64
一般的科学计算尽量使用 float64 (double)数据类型,会省去很多麻烦(跃过大数吃小数、相近数相减的陷阱)。
GPU (图形处理单元,简称显卡) 并行编程时,为了加快运算,一般使用 float32 而不是 double(或称 float64) 类型。
目前的人工智能(深度学习)库,有时甚至使用 float16 数据类型。
大数加小数困难的解决方案¶
为了计算速度考虑,如果不想用 double(即 float64)数据类型,又希望大量数字的求和结果比较精确, 可以考虑使用如下两种方案:
- Kahan 求和公式(解决串行求和时大数吃小数的问题)
- 将串行求和转化为并行求和
Kahan 求和原理¶
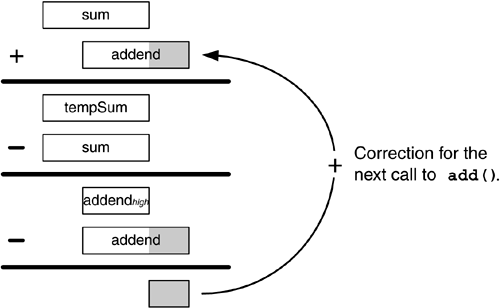
def kahan_sum(arr):
'''连加操作中解决大数吃小数的问题
:arr: numpy array,存储 float 类型
:return: arr 中所有元素的和'''
sum_ = np.float32(0)
correction = np.float32(0)
for addend in tqdm(arr):
addend += correction # <--
temp_sum = sum_ + addend # \
addend_high = temp_sum - sum_ # \
correction = addend - addend_high # --
sum_ = temp_sum # update
return sum_
#举例
arr = np.ones(int(1.0E6), dtype=np.float32) * 1.0E-6
sum_ = np.float32(0)
for x in tqdm(arr):
sum_ += x
print("sum(arr)=", res)
kahan_sum(arr)
避免两个相近的数相减¶
有时候可能会遇到两个相近数的相减,比如计算数值微分时,使用如下公式
\begin{align} {d f \over dx} = {\rm lim}_{h \rightarrow 0} {f(x + h) - f(x) \over h} \end{align}从微分的定义来看, $h$ 越小,$df/dx$ 的计算越精确。
但 $h$ 越小,$f(x+h)$ 与 $f(x)$ 越接近,会出现相近数的相减问题。
举例:$f(x) = \sqrt{x}$, 此时 f(x) 对 x 的导数为, \begin{align} {df \over dx} = {1 \over 2} x^{-1/2} \end{align}
在 x = 1 处,${df \over dx} = 0.5$.
def f(x):
#return np.sqrt(x)
return np.sqrt(x).astype(np.float32)
def dfdx(func, x=1, h=1.0E-6):
return (func(x+h) - func(x))/h
print("h=0.01, dfdx=", dfdx(f, h=0.01))
print("h=0.001, dfdx=", dfdx(f, h=0.001))
print("h=1.0E-6, dfdx=", dfdx(f, h=1.0E-6))
print("h=1.0E-9, dfdx=", dfdx(f, h=1.0E-9))
几个避免相近数相减的替换方案(数值分析,李红):
\begin{align} \sqrt{x+\epsilon} - \sqrt{x} &= {\epsilon \over \sqrt{x + \epsilon} + \sqrt{x}} \\ \ln (x+\epsilon) - \ln(x) &= \ln(1 + {\epsilon \over x}) \\ {\rm for\ |x|\ll 1},\ e^x -1 &= x \left( 1 + {x \over 2} + {x^2 \over 6} + \cdots \right) \\ {\rm for\ |x|\ll 1},\ 1 - \cos x &= 2 \sin^2 {x \over 2} \end{align}避免两个浮点数的相等(==)比较¶
因为计算机上浮点数有舍入误差,对浮点数做 == 比较有时会出现不可预测的错误。
举例:
a = 3.14159268
b = 3.14159269
判断 a==b 返回 True 还是 False?
对于 float32 类型,最后的 8 和 9在舍入误差上,我们希望它返回 True
# 默认使用 float64 类型
a = 3.14159268
b = 3.14159269
a == b
# 比较好的做法是 np.isclose() 或 np.allclose() 函数
# 尤其是在对比数值解与解析解时
np.isclose(a, b)
# 使用 np.isclose(SHIFT + TAB), 在函数括弧处按 SHIFT+TAB 键看函数介绍
# 或 help(np.isclose)
NaN (Not A Number) 和 inf ($\infty$)¶
自己辛苦编写了一长串程序,结果却输出 nan,怎么办?注意下面这些情形,
- $1 \over x$, x=0
- $\sqrt{x}$, x<0
- $\log(x)$, x<0
- $\exp(x)$, x 非常大
import numpy as np
x = np.sin(3/2 * np.pi)
# 根号下出现了负值
y = np.sqrt(x)
np.sin(y)
print("x =", x)
# 负数开 4 次方,或其他偶数次方
x**(1/4)
x = np.sin(0)
100 / x
# 根据粒子出射动量 (px, py),计算方位角
def phi(px, py, wrong_method=False):
'''计算出射角度
:px: 动量的 x 分量
:py: 动量的 y 分量
:return: 方位角 [-pi, pi)'''
return np.arctan2(py, px)
# 注意:不能使用 np.arctan(py/px) 函数
# 因为,如果粒子沿 y 轴出射, px==0,
# py/px 会出现“除零错误”
print("phi(px=0, py=1)=", phi(0, 1))
print("phi(px=-1, py=0)=", phi(-1, 0))
print("phi(px=0, py=-1)=", phi(0, -1))
def phi_wrong(px, py):
'''这是错误的计算粒子出射方位角方法'''
return np.arctan(py/px)
phi_wrong(px=0, py=1)
# 处理办法:
# (1)加 assert 在 x < 0 时直接报错,不继续进行计算
# (2)或者使用 异常 捕获机制
x = -1
assert(x > 0)
np.sqrt(x)
预估任务复杂度,内存与硬盘占用¶
有时候写了一个程序,结果运行起来永不停歇,或者爆出内存不够、显存不够或磁盘空间不够。
为了预防这些问题,要对任务复杂度、内存和硬盘占用进行预估。
举例:N 个带电粒子的分子动力学模拟,每一步需要计算每一对粒子之间的库伦相互作用,有 $\sim{\mathcal O}(N^2)$ 次操作.
对于 1 GHZ 的电脑CPU,每秒浮点数操作次数为 $10^9$,假设遍历一次需要 $10^{-9}$ 秒,可以估算每一步花费时间,
$N^2 \times 10^{-9}$ s
import matplotlib.pyplot as plt
def plot_time(dt = 1.0E-9):
N = np.logspace(1, 6)
t = N**2 * dt
plt.loglog(N, t)
plt.xlabel("num of particles")
plt.ylabel("cpu time (s)")
plot_time()
内存、显存与硬盘占用¶
举例:假设电脑的可用内存为 1 GB,做三维相对论流体力学计算需要将空间离散化为
${\rm Nx \times Ny \times Nz} = 1000 \times 1000 \times 1000$ grids
问:如果使用 float32 类型数据,内存是否够用?
1G = $10^9$, 1 M(兆) = $10^6$
1 Byte(字节) = $8$ bits(位)
1 float32 = 4 Byte
1 float64(double) = 8 Byte
假设每个格子上只保存一个浮点数,
${\rm Nx \times Ny \times Nz} = 10^{9}$ 个格子上的 float32 类型浮点数占用内存为 4 GB, 显然内存不够用。
如果设 ${\rm Nx=300, Ny=300, Nz=300}$,
则内存占用为 108 兆比特,明显够用。
$\rm 27\ M\ float32 \times 4\ B/float32 = 108\ MB$