冯康与哈密顿系统的辛几何算法¶
庞龙刚@华中师范大学
学习内容¶
- 冯康是谁
- 什么是哈密顿系统
- 什么是辛算法 (Symplectic Algorithm)
- 常微分方程的传统解法
%matplotlib inline
from IPython.display import Image
import matplotlib.pyplot as plt
import numpy as np
# odeint 用于求解常微分方程
from scipy.integrate import odeint
plt.style.use(['science', 'notebook', 'no-latex'])
冯康是谁¶
冯康(1920-1993)是中国科学院院士,计算数学奠基人。
美籍华人数学家、菲尔兹奖获得者丘成桐说:“中国近代数学能超越西方或与之并驾齐驱的主要原因有三个,
一个是陈省身在示性类方面的工作,
一个是华罗庚在多复变函数方面的工作,
一个是冯康在有限元计算方面的工作。”
冯康除了独立西方提出有限元算法外,还有一项不太被人知道的成就:
哈密尔顿系统的辛几何算法,被追授为“1997年国家自然科学奖一等奖”。
详细参考:
- 《冯康传》
- 《Symplectic Geometry Algorithms for Hamiltonian Systems》, by Kang Feng, Mengzhao Qin
Image("images/fengkang_photo.png", height="500")
Image("images/fengkang_words.png", height="500")
# 数值解需要尽量遵从问题本身的对称性和守恒律
# 物理定律有各种各样的表示和计算方法
# 不同的计算方法可能产生不同的数值结果
# 接下来以哈密顿系统和辛几何算法展示这段话的含义
什么是哈密顿 (Hamilton) 系统¶
哈密顿系统是耗散可忽略不计的真实物理系统,无论它是经典的、量子的、相对论性的、有限维还是无限维的系统。
哈密顿系统的演化满足两类守恒律,
- 能量守恒、动量守恒、角动量守恒
- 相空间(坐标、动量)的面积守恒(Liouville–Poincar´e conservation law)
举例:行星系统,双原子分子的经典轨道,封闭量子系统(closed quantum system),无阻尼谐振子
在冯康之前,很少有人考虑两个问题,(1). 现有的数值算法是否适用于哈密顿系统 (2). 如果不适用,如何构造适用于哈密顿系统的数值算法
比如,为了计算行星轨道,需要数值求解如下哈密顿运动方程,其中哈密顿量为 $H = T + V$。
\begin{align} {d q \over dt} &= {\partial H \over \partial p} \\ {d p \over dt} &= - {\partial H \over \partial q} \end{align}如果需要模拟几十万年的时间,数值计算结果能否真正反映物理现实。
如果因为数值耗散,导致行星逐渐坠入太阳,或逐渐脱离太阳系,我们能否信任这样的模拟结果?
如何构造“干净”的数值算法,使得数值求解过程满足哈密顿系统的两类守恒律?
Image("images/kapler_symplectic.png")
# 开普勒系统:行星轨道
# (a) 传统算法,行星轨道不封闭,
# (b) 辛几何算法, 稳定封闭轨道
Image("images/Li2.png")
# Li2 双原子系统的经典轨道
# 第一行为辛算法(symplectic method), 长时稳定,振幅,周期性,总能量,相轨道都保持良好
# 第二行为龙格库塔(R-K) 算法, 5000 个时间步之后振幅变小,总能量下降
举例:无阻尼谐振子
假设地面无限光滑,弹簧无热耗散。
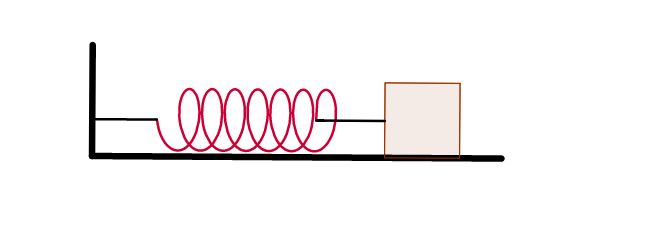
如果拉伸弹簧后松开,方块儿会永不停歇的做简谐振动。
这个最简单的谐振子系统的哈密顿量为,
$H = {p^2 \over 2 m } + {k q^2 \over 2}$
其中
- $p$ 是方块儿的动量,
- $m$ 是方块儿的质量,
- $k$ 是弹簧的弹性系数,
- $q$ 是方块儿位移,表示弹簧拉伸或压缩的长度,有时候也用 $x$ 表示。
定义弹簧拉伸/压缩长度为 0 时,方块的坐标 $q=0$。
经典力学哈密顿量可以看做是给定状态下系统的能量,等于动能 $T(q)$ 加势能 $V(q)$。
$E = T(p) + V(q) = {p^2 \over 2 m } + {k q^2 \over 2}$
将 E 除到右边,上面方程表现出很奇特的性质,
$ {p^2 \over 2 m E } + {k q^2 \over 2 E} = 1$
如果设 $a^2 = 2 m E$, $b^2 = 2E/k$, 上面的方程变为,
$ {p^2 \over a^2 } + {q^2 \over b^2} = 1$
这是一个椭圆的轨迹方程。
即坐标和动量$(q, p)$ 轨道在相空间中是一个等能量的椭圆!
如果推广到高维系统,就是等能面。有些地方也把它叫做叫“辛流形” (Symplectic Manifold)。
下面先画一下理想情况下方块儿的相空间(坐标,动量)轨迹,选择两个不同的弹性系数 $k$。
将 $q, p$ 重新参数化为,
\begin{align} q = b \cos \theta \\ p = a \sin \theta \end{align}可以看到它们满足 $ {p^2 \over a^2 } + {q^2 \over b^2} = 1$。 不同的 $\theta$ 对应相空间不同的点。
def phase_flow(E, mass, k, theta=0):
'''产生等能面上的初始条件 (q, p)
:E: 能量,>0
:mass: 质量 >0
:k: 弹簧弹性系数 > 0
:return: (q, p) 相轨(相流)的解析解'''
a = np.sqrt(2 * mass * E)
b = np.sqrt(2 * E / k)
q = b * np.cos(theta)
p = a * np.sin(theta)
return q, p
# 绘制理想情况下方块儿在相空间中的轨迹
# (q, p) 表示方块儿的位移与动量,对于不同的弹簧弹性系数,相空间轨迹是不同的椭圆。
# 下面这两个相空间轨迹分别对应能量 E=1, 质量 m=1, 弹性系数 k=1 和 2。
# 我们希望数值解出的 (q, p) 也在这个等能面上,无论模拟的时间有多长。
theta = np.linspace(0, 2*np.pi, 100)
q1, p1 = phase_flow(E=1, mass=1, k=1, theta=theta)
q2, p2 = phase_flow(E=1, mass=1, k=2, theta=theta)
plt.plot(q1, p1, 'k-', label="k=1")
plt.plot(q2, p2, 'r--', label="k=2")
plt.xlabel('q')
plt.ylabel('p')
plt.legend(loc='best')
plt.gca().set_aspect('equal')
从哈密顿量可以得到运动方程,
${d q \over dt} = {\partial H \over \partial p}= {p \over m}$
${d p \over dt} = - {\partial H \over \partial q} = - k q$
这两个方程分别是小球的速度和动量(加速度)满足的时间演化方程。
简单起见,设 $m=1, k=1$, 写成矩阵的形式,
${d \over d t} \begin{bmatrix} q \\ p \end{bmatrix} = \begin{bmatrix} p \\ -q \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} q \\ p \end{bmatrix} $
这种 $J = \begin{bmatrix} 0 & I \\ -I & 0 \end{bmatrix}$ 斜对角矩阵是一个非常有意思的结构,
正交矩阵 R 定义为满足 $R^T R = R^T I R = I$ 的实矩阵,它们是 $O(n)$ 群的群元。
可以证明所有满足 $M^T J M = J$ 的 2n*2n 的实矩阵(或称变换)$M$ 也构成一个群,这个群叫辛群, 记为 Sp(2n, R)。
证明满足 $M^T J M = J$ 的所有 2n*2n 实矩阵 $M$ 构成一个群需要证明,
- 存在单位元 : 2n*2n 的单位矩阵 I 满足 $I^T J I = J$
- 存在逆元: 如果 M 是这个群的元素,即 $M^T J M=J$, 则 $(M^{-1})^{T} J M^{-1} = (M^{-1})^{T} M^T J M M^{-1} = (M M^{-1})^T J (M M^{-1}) = I^T J I = J$, 说明 $M^{-1}$ 也是这个群的元素。
- 如果 $M_1$, $M_2$ 分别是这个群的元素,则$M_1 M_2$ 也是这个群的元素。
由上面两个条件推导出, \begin{align} J = M_2^T J M_2 &= M_2^T M_1^T J M_1 M_2 = (M_1 M_2)^T J (M_1 M_2) \end{align} 即 $M_1M_2$ 也是这个群的元素。注:推导过程多处用到 $(A B)^T = B^T A^T$
为了保证数值解不会因为误差累积而偏离等能面,需要数值离散格式的每一步更新变换矩阵 $M$ (或称雅克比矩阵)是辛群的一个元素。
$M = {\partial (q^*, p^*)\over\partial (q, p)} = \begin{bmatrix} {\partial q^* \over \partial q} & {\partial q^* \over \partial p} \\ {\partial p^* \over \partial q} & {\partial p^* \over \partial p} \end{bmatrix}$
即 $M^T J M = J$ 成立表示数值离散格式是“保辛算法”。
显式欧拉法 (Explicit Euler)¶
首先检查不用辛几何算法,而是使用显式欧拉法 (Explicit Euler)解谐振子问题,会得到何种结果。
设 $y=\begin{bmatrix} q \\ p \end{bmatrix}$, $f(y, t)=\begin{bmatrix} p \\ -q \end{bmatrix}$, 则运动方程${d \over d t} \begin{bmatrix} q \\ p \end{bmatrix} = \begin{bmatrix} p \\ -q \end{bmatrix} $可以写为标准的常微分方程形式
\begin{align} {d y \over dt} = f(y, t) \end{align}显式欧拉法做向前差分近似 ${dy \over dt} \approx {y^{n+1} - y^n \over h}$ ,则常微分方程离散化为,
\begin{align} y^{n+1} = y^{n} + h f(y^n, t_0 + n h) \end{align}其中 $y^n$ 表示第 n 个时间步时 y 的值,时间步长 $ h = \Delta t$.
# 第一步:为了求解常微分方程,我们首先需要设定初始条件
# 设 t=0 时,方块儿位移最大, q = b cos(theta=0) = b
q0, p0 = phase_flow(E=1, mass=1, k=1, theta=0)
print("初始条件:(q, p)=(%.2f, %.2f)"%(q0, p0))
# 第二步:按照 Explicit Euler 格式更新方块儿的坐标和动量
# 先定义 dy/dt = f 的右边, f = [p, -q]^T
def f(y, t):
'''
:y: 广义坐标与动量 [q, p]
:return: 运动方程 [p, -q]'''
return np.array([y[1], -y[0]])
def explicit_euler(f, y0, t):
'''显式欧拉法计算相空间轨迹
:f: 函数 f(y, t), 常微分方程dy/dt = f 的右边
:y0: 初始条件, y(t[0])
:t: np.array(), 长度等于时间步数
:return: 常微分方程的解 '''
dt = t[1] - t[0]
sol = [y0]
y = y0
for ti in t[1:]:
y = y + dt * f(y, ti)
sol.append(y)
return np.array(sol)
y0 = np.array([q0, p0])
tmax, nsteps = 100, 10000
t = np.linspace(0, tmax, nsteps)
# sol 是显式欧拉法求解结果
sol = explicit_euler(f, y0, t)
print("The shape of the solution is:", sol.shape)
plt.plot(t, sol[:, 0])
plt.xlabel("time")
plt.ylabel("q")
# 显式欧拉法: 谐振子的振幅越来越大,不符合物理现实!
def plot_phase_flow(sol, title="tmax=100, dt=0.01", style='k-', label=''):
q = sol[:, 0]
p = sol[:, 1]
plt.plot(q, p, style, lw=1, label=label)
plt.xlabel('q')
plt.ylabel('p')
plt.title(title)
plt.gca().set_aspect('equal')
theta = np.linspace(0, 2*np.pi, 100)
q1, p1 = phase_flow(E=1, mass=1, k=1, theta=theta)
plt.plot(q1, p1, 'k-', label="analytic")
plot_phase_flow(sol, style='r--', label='explicit euler')
plt.legend(loc='best')
举例:判断显式欧拉法离散格式的变换矩阵是否为辛群的元素¶
对于之前的问题, \begin{align} {d \over d t} \begin{bmatrix} q \\ p \end{bmatrix} = \begin{bmatrix} p \\ -q \end{bmatrix} \end{align} 将上述运动方程离散化后,得到更新变换,
\begin{align} q^{n+1} = q^n + h\ p^n \\ p^{n+1} = p^n -h\ q^n \end{align}更新变换矩阵为, \begin{align} M = {\partial (q^{n+1}, p^{n+1})\over\partial (q^n, p^n)} = \begin{bmatrix} 1 & h \\ -h &1 \end{bmatrix} \end{align} 可以简单验证 $M^T J M \neq J$, 对于此问题,显式欧拉法离散格式不是保辛格式。
from sympy import Matrix
from sympy import symbols
import sympy as sym
h = symbols("h")
M = Matrix([[1, h], [-h, 1]])
J = Matrix([[0, 1], [-1, 0]])
M.T @ J @ M
# 雅可比矩阵的行列式表示变换后相空间体积的增大倍数
# 保辛算法的另一个特点: det(M)**2 = 1
# 显式欧拉法的 det(M)**2 > 1, 所以振幅越来越大
M.det()**2
但是对于某些问题,显式欧拉法又是保辛格式,比如,假设存在如下常微分方程组,
\begin{align} {dq \over dt} &= 0 \\ {dp \over dt} &= f(q) \end{align}离散化格式为, \begin{align} q^{n+1} &= q^n \\ p^{n+1} &= p^n + h f(q^n) \end{align}
更新变换矩阵为, \begin{align} M &= {\partial (q^{n+1}, p^{n+1})\over\partial (q^n, p^n)} = \begin{bmatrix} 1 & 0 \\ h f'(q) &1 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ a &1 \end{bmatrix} \end{align} 其中,最后一步我们设 $ h f'(q)=a$。
a = symbols("a")
M = Matrix([[1, 0], [a, 1]])
M.T @ J @ M
M.det()**2
对于特定的问题,判断 M 是否是辛群的元素,从而可以知道离散化格式是否保辛。
这是群论在数值计算稳定性判断中的重要应用。
最简单的辛欧拉算法¶
对于动能与势能可分的哈密顿量,存在一个非常简单的辛欧拉离散化格式。只需要在原始的欧拉算法上做个微调,
\begin{align} q^{n+1} &= q^n + h\ p^{n+1} \\ p^{n+1} &= p^n -h\ q^n \end{align}这里相当于隐式的使用下一时刻的动量 $p^{n+1}$ 更新坐标 $q^{n+1}$。 将第一式中 $p^{n+1}$ 移到左边,将第二式乘以 h,与第一式相加,
\begin{align} q^{n+1} - h p^{n+1} &= q^n \\ h p^{n+1} &= h p^n -h^2\ q^n \end{align}得到更新步骤,
\begin{align} q^{n+1} &= (1- h^2) q^n + h p^n \\ p^{n+1} &= - h q^n + p^n \end{align}写成矩阵形式,
\begin{align} y^{n+1} = M y^n = \begin{bmatrix} 1-h^2 & h \\ -h &1 \end{bmatrix}\begin{bmatrix} q^n \\ p^n \end{bmatrix} \end{align}此时更新变换矩阵为, \begin{align} M = {\partial (q^{n+1}, p^{n+1})\over\partial (q^n, p^n)} = \begin{bmatrix} 1-h^2 & h \\ -h &1 \end{bmatrix} \end{align}
可以简单验证 $M^T J M = J$, 从而证明这种格式确实为辛欧拉格式。
M = Matrix([[1-h*h, h], [-h, 1]])
M.T@J@M
M.det()
#接下来我们使用“辛欧拉算法测试谐振子问题
def symplectic_euler(f, y0, t):
'''辛欧拉算法计算相空间轨迹
:f: 函数 f(y, t), 常微分方程dy/dt = f 的右边
:y0: 初始条件, y(t[0])
:t: np.array(), 长度等于时间步数
:return: 常微分方程的解 '''
h = t[1] - t[0]
sol = [y0]
q, p = y0
for ti in t[1:]:
p = p - h * q
q = q + h * p
sol.append([q, p])
return np.array(sol)
sol = symplectic_euler(f, y0, t)
print("The shape of the solution is:", sol.shape)
plt.plot(t, sol[:, 0])
plt.xlabel("time")
plt.ylabel("q")
plt.title("Symplectic Euler Method")
# 辛欧拉法: 谐振子的振幅保持恒定
plt.plot(q1, p1, 'k-', label="analytic")
plot_phase_flow(sol, title="tmax=50, dt=0.01", style='r--', label='symplectic euler')
plt.legend(loc='best')
欧拉中点辛算法¶
有些书上介绍了另一种方法 -- 欧拉中点法,算法步骤如下,
设 $y = \begin{bmatrix} q \\ p \end{bmatrix}$, 如果 Hamilton 矩阵可以写成 $y$ 的二次型,即
\begin{align} H = {1 \over 2}y^T C y \end{align}且 $C^T = C$, 则存在一个简单的辛欧拉公式,
\begin{align} y^{n+1} &= M y^n \\ M &= \left( 1 - {h \over 2}B \right)^{-1} \left( 1 + {h \over 2}B \right) \end{align}其中 $B = J C$。
很明显之前的谐振子例子满足辛欧拉算法的使用条件,
$ C = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}$,
$ H = {1 \over 2} \begin{bmatrix} q^T & p^T \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix} q \\ p \end{bmatrix} = {1 \over 2}y^T C y$,
$ B = J C = \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} = J $
B = J
I22 = Matrix([[1, 0], [0, 1]])
M = (I22 - h/2 * B).inv() @ (I22 + h/2 * B)
M = sym.simplify(M)
M
sym.simplify(M.det())
# 保相空间体积
sym.simplify(M.T @ J @ M)
# 可以看到 M.T@J@M == J,保辛
这个辛欧拉格式的得出过程为,
\begin{align} \dot{y} &= {d y \over dt} \\ &= J {\partial_y H } = J { \partial_y \left({1 \over 2}y^T C y \right)} \\ &= JC y = B y \end{align}然后使用欧拉中点法,
\begin{align} y^{n+1} - y^n = {h B \over 2} (y^{n+1} + y^n) \end{align}即可得到步进公式, $M = \left( 1 - {h \over 2}B \right)^{-1} \left( 1 + {h \over 2}B \right)$。
实际使用中发现此格式对谐振子问题并不友好,同学们可以寻找一下公式推导中是否有 bug。
常微分方程的常规解法:龙格库塔¶
如果是短时模拟,或者求解的系统不是哈密顿系统(有时也称保守系统),最常用的解常微分方程的方法是龙格库塔(Runge-Kutta 法)。
对于常微分方程, \begin{align} {d y \over dt} = f(y, t) \end{align}
Runge-Kutta 方法使用区间 $[t^n, t^{n+1}]$ 上多个点的梯度 $f$ 得到一个平均梯度,来提高数值求解精度,
\begin{align} y^{n+1} = y^n + h \sum_{i=1}^L \lambda_i k_i \end{align}比如,Runge-Kutta 算法中最常用的 4 级 4 阶公式,可以展开为,
\begin{align} y^{n+1} &= y^n + {h \over 6}(k_1 + 2k_2 + 2k_3 + k_4) \\ k_1 &= f(t^n, y^n) \\ k_2 &= f(t^n + {h \over 2}, y^n + {h \over 2} k_1) \\ k_3 &= f(t^n + {h \over 2}, y^n + {h \over 2} k_2) \\ k_4 &= f(t^n + h, y^n + h k_3) \end{align}练习:可以尝试实现 4 阶 Runge-Kutta 公式,并与显式欧拉法结果对比。
一般情况下,并不需要我们自己实现 Runge-Kutta 算法,Python,Mathematica 或者 Matlab 中都有成熟的实现。
动画对比不同算法求解哈密顿系统的常微分方程¶
%matplotlib notebook
from matplotlib.animation import FuncAnimation
tmax = 20
tsteps = 1000
dt = tmax / tsteps
sol = explicit_euler(f, y0, t)
#sol = odeint(f, y0, t)
#sol = symplectic_euler(f, y0, t)
def update(i):
q = sol[0 : i, 0]
p = sol[0 : i, 1]
line1.set_data(q, p)
line2.set_data(sol[i, 0], sol[i, 1])
text.set_text(r'$t=%.2f$'%(i*dt))
return line1, line2, text,
fig1, ax1 = plt.subplots()
# 画等能面,数值解要在等能面上
theta = np.linspace(0, 2*np.pi, 100)
q_ana, p_ana = phase_flow(1, 1, 1, theta)
plt.plot(q_ana, p_ana)
# 画历史轨迹
line1, = plt.plot(sol[0, 0], sol[0, 1], 'ro', ms=1)
# 画当前相空间位置
line2, = plt.plot(sol[0, 0], sol[0, 1], 'ko', ms=5)
text = plt.text(-6, 6, '')
#plt.title("Symplectic Euler Method")
plt.grid(ls="--")
plt.ylabel(r'$p$')
plt.xlabel(r'$q$')
plt.gca().set_aspect('equal')
anim1 = FuncAnimation(fig1, update, frames=10000, interval=10, blit=False)
#anim1.save('images/symplectic_euler_anim.mp4')
#plt.show()