当物理学遇上人工智能
Long-Gang Pang, IOPP@CCNU
2020-08-09, CCNU (注:按 f 键全屏)
内容
- 人工智能简介
- 应用场景
- 原理简介
- 可解释性
- 不确定性
- AI 伦理
- 学习资源
- 物理遇上人工智能
- 物理中的反问题
- 物理中的变分问题
- 物理中的生成问题
- 物理对深度学习的启发
人工智能简介
人脸识别 (Who)

身份认证, 刷脸支付
图像语义分割 (What and where)

智能医疗,智能农业,智能工业,自动驾驶
人工智能发展里程碑

2016年3月,AlphaGo 打败围棋前世界冠军李世石
自我对弈训练的 AlphaGo Zero
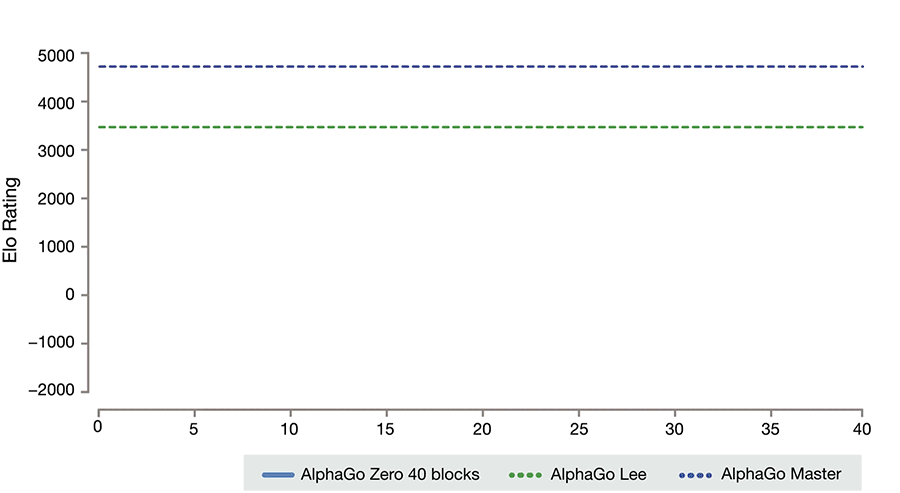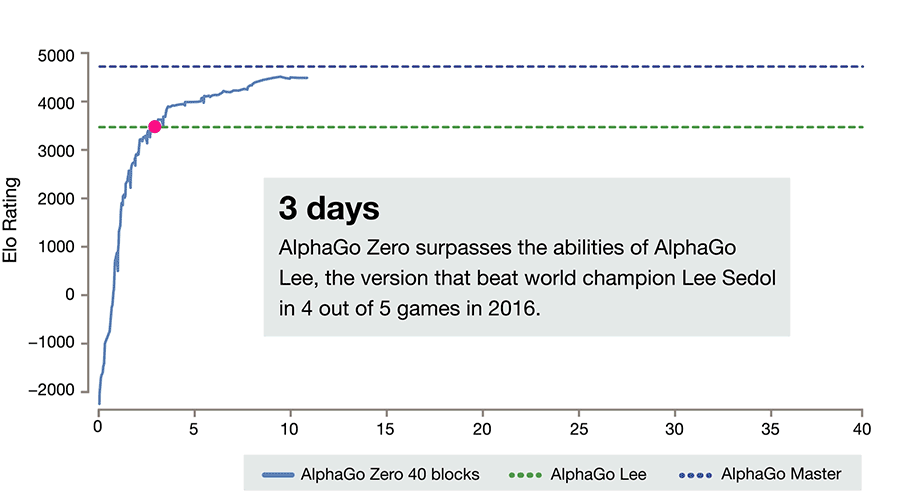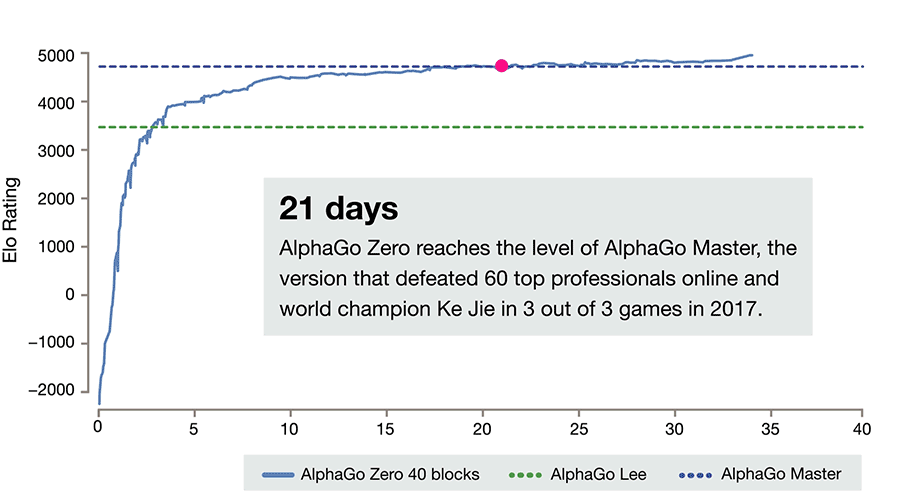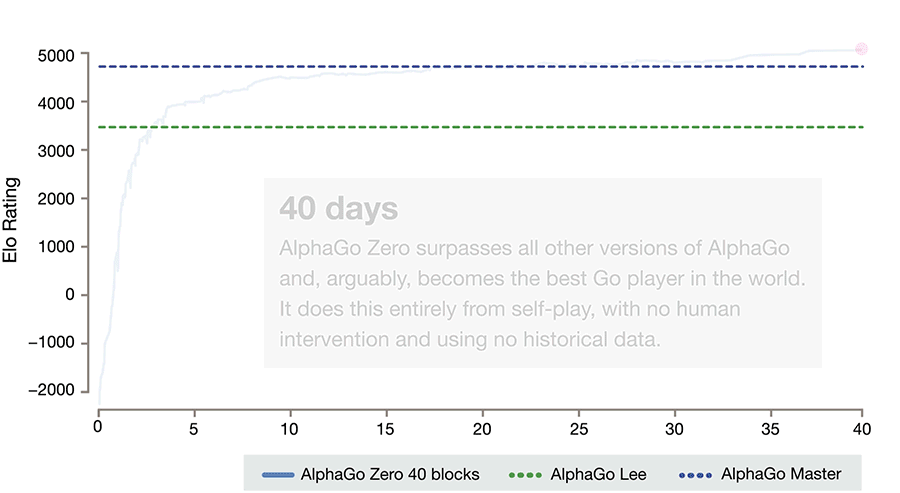
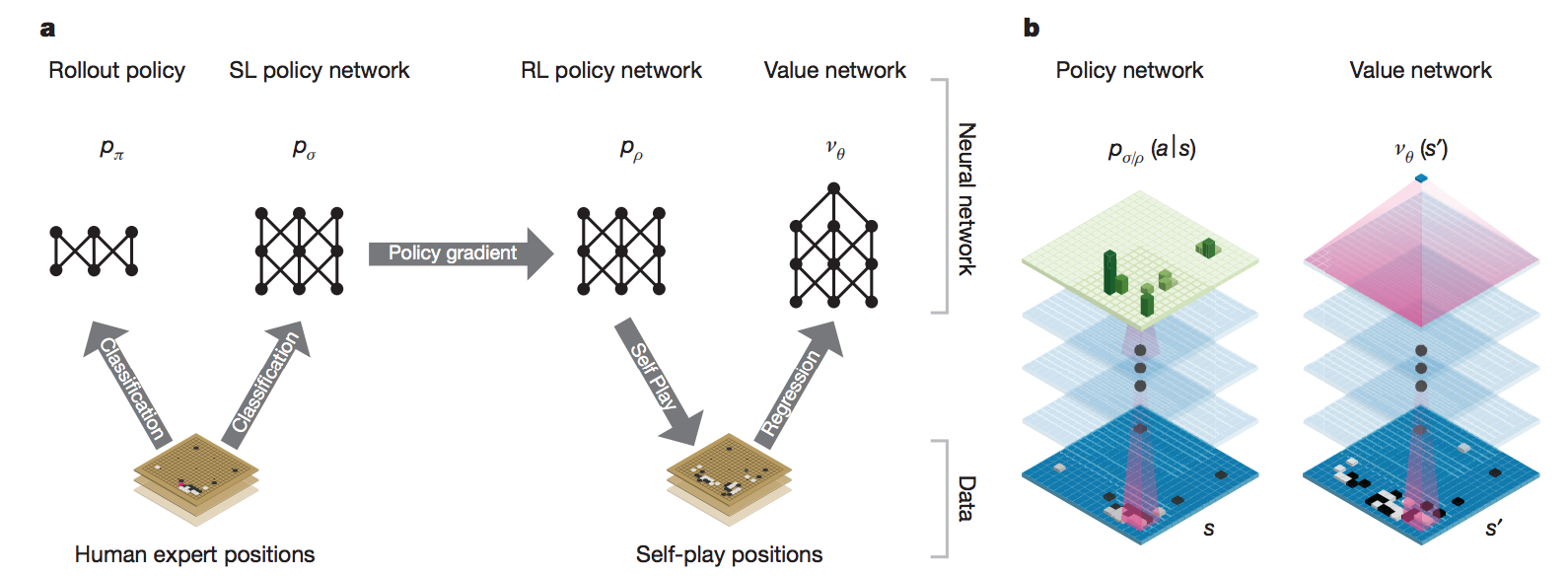
战略网络(Value Network)与战术网络(Policy Network)
自然语言处理

图像风格转化

新冠肺炎识别
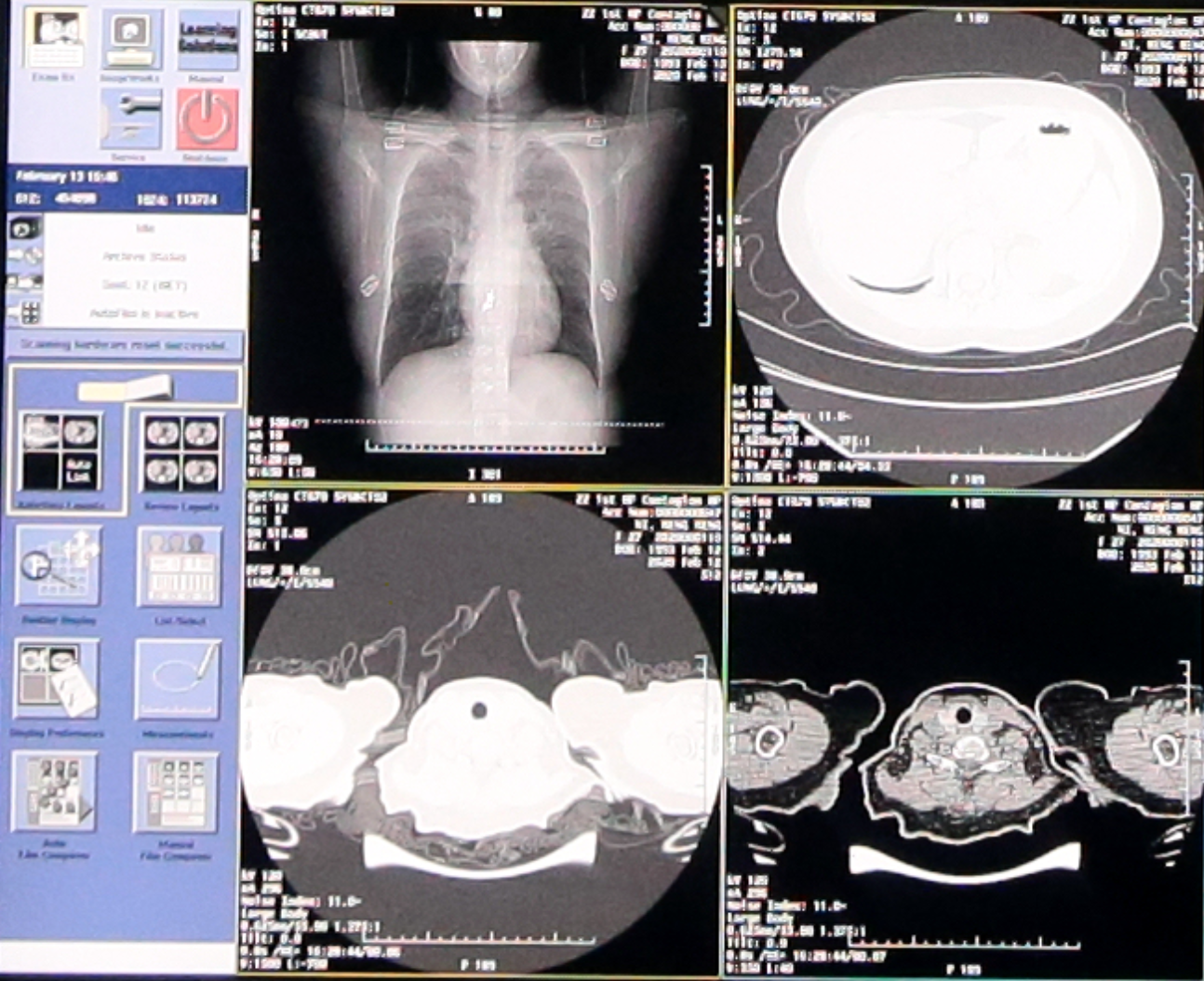
阿里达摩院,腾讯,华为…
这些黑科技背后的人工智能技术 – 深度学习
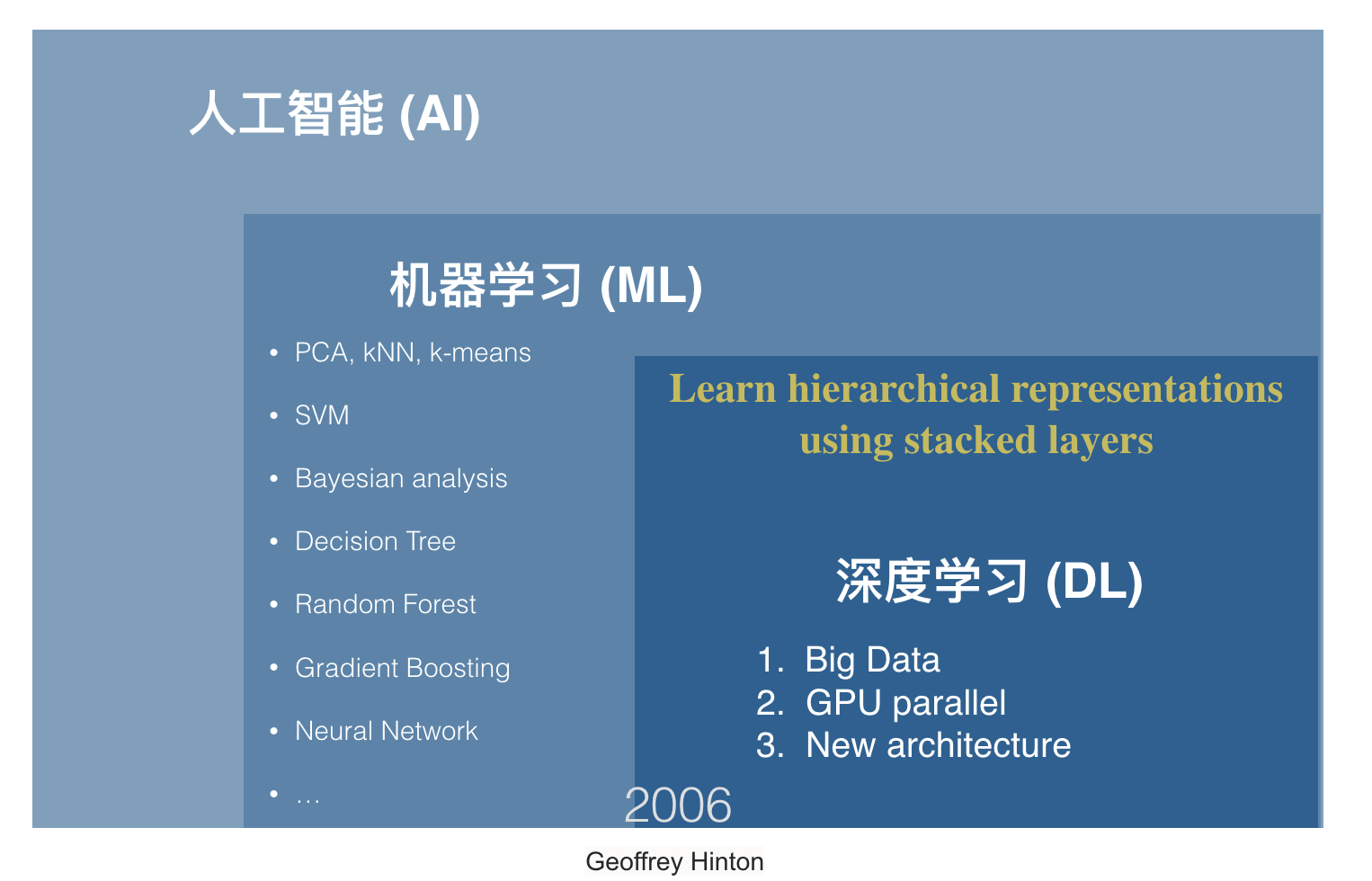
深度学习是什么
- 深度学习是机器学习的子集
- 机器学习是人工智能的子集
- 机器学习:不对特定任务编程,计算机自动从数据中学习
- 深度学习:层级化的泛函模块,拥有更强的表示能力
- 目前的深度学习属于弱人工智能,强于感知,弱于推理
深度学习是一种新的编程模式
传统编程模式: 输入 + 预设指令 = 输出
自动编程模式: 输入 + “混乱大脑” + 输出 = “条件反射大脑”
深度学习是什么
深度学习分类
- 监督学习 (Supervised Learning)
- 非监督学习 (Unsupervised Learning)
- 自监督学习 (Self-supervised learning)
- 半监督学习 (Semi-supervised learning)
- 强化学习 (Reinforcement learning)
- 主动学习 (Active learning)
- 元学习 (Meta learning)
人类大脑的启发

对大部分人来说,深度学习 = 多层人工神经网络
生物神经元
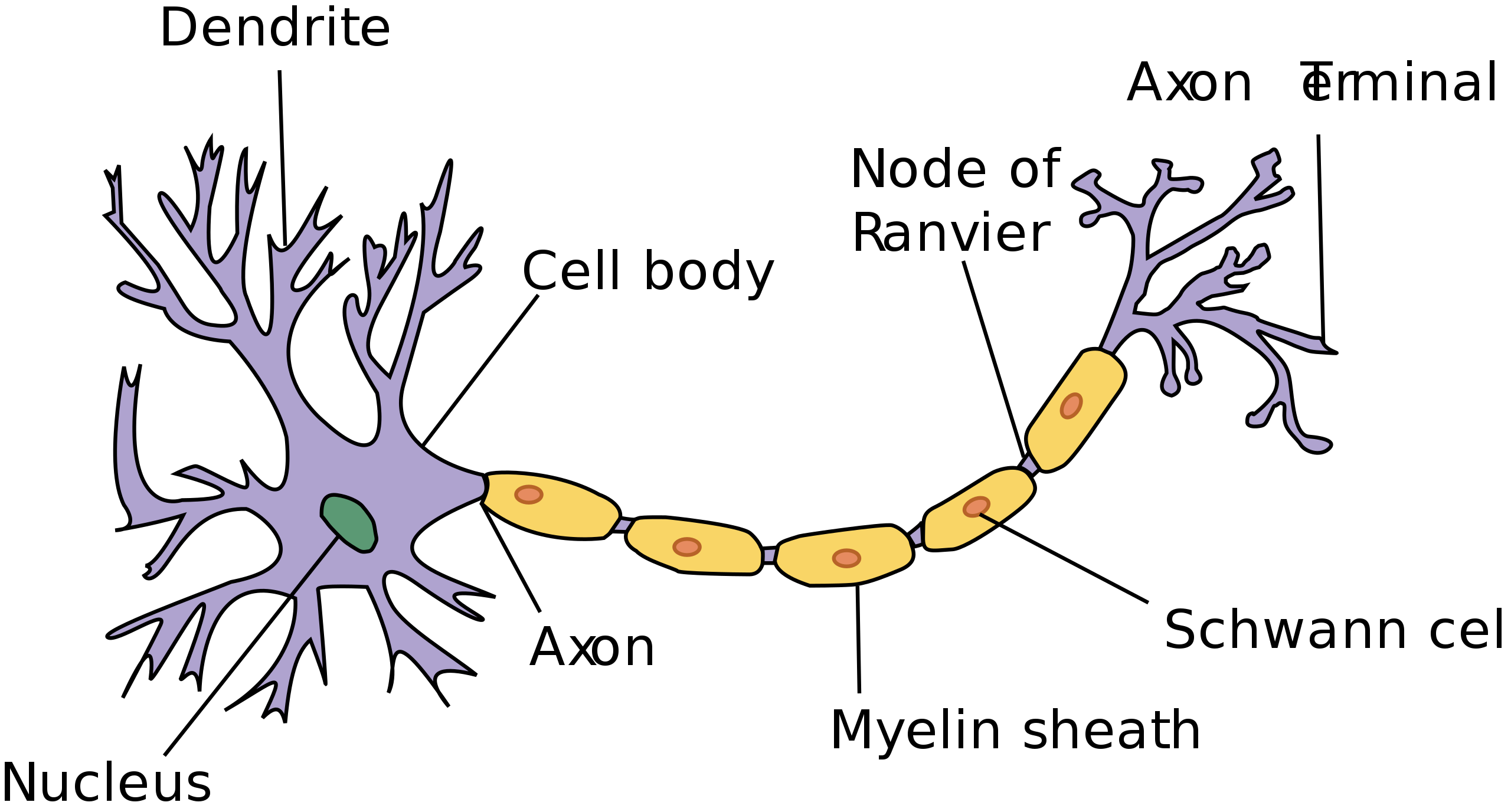

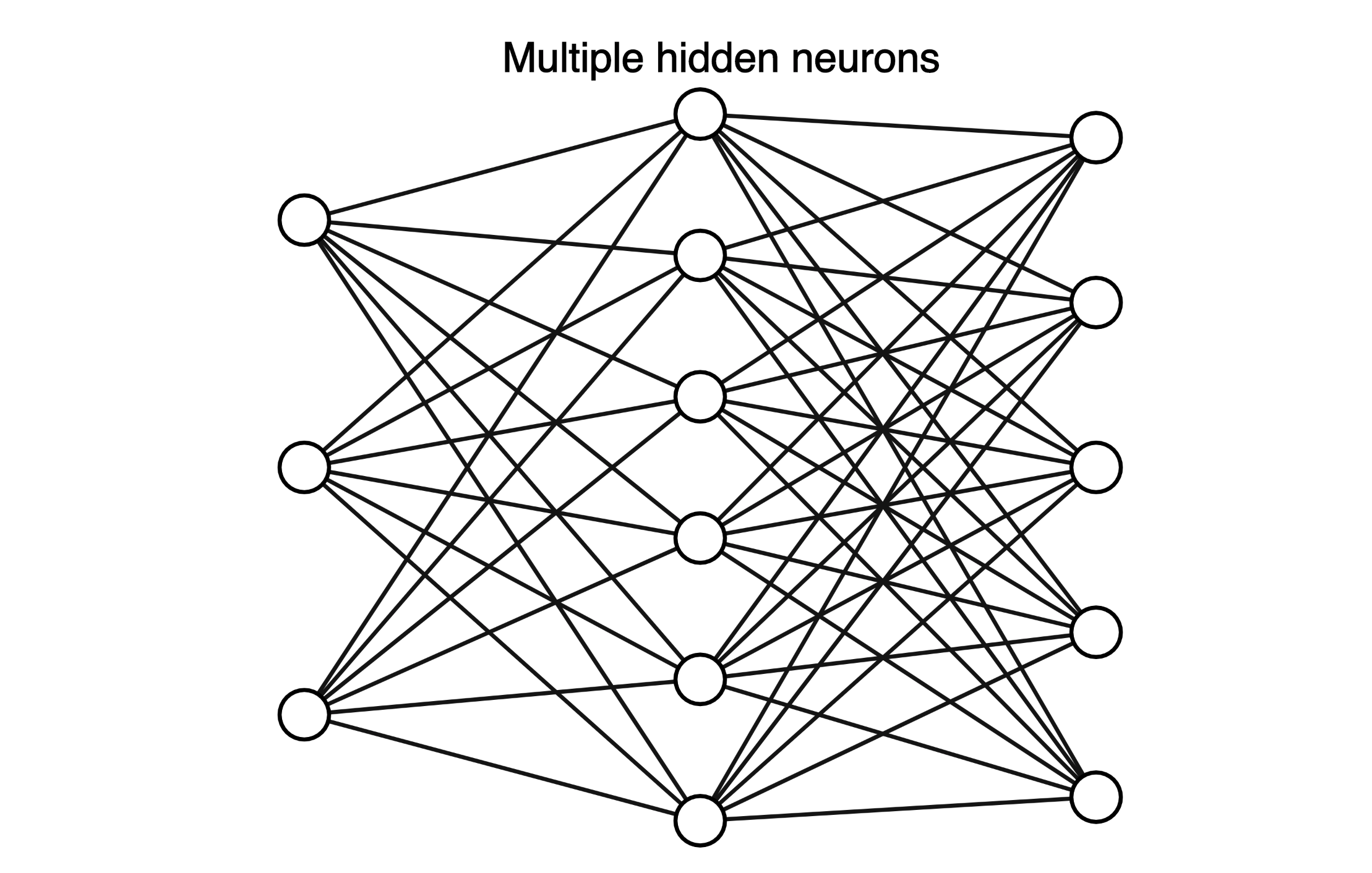
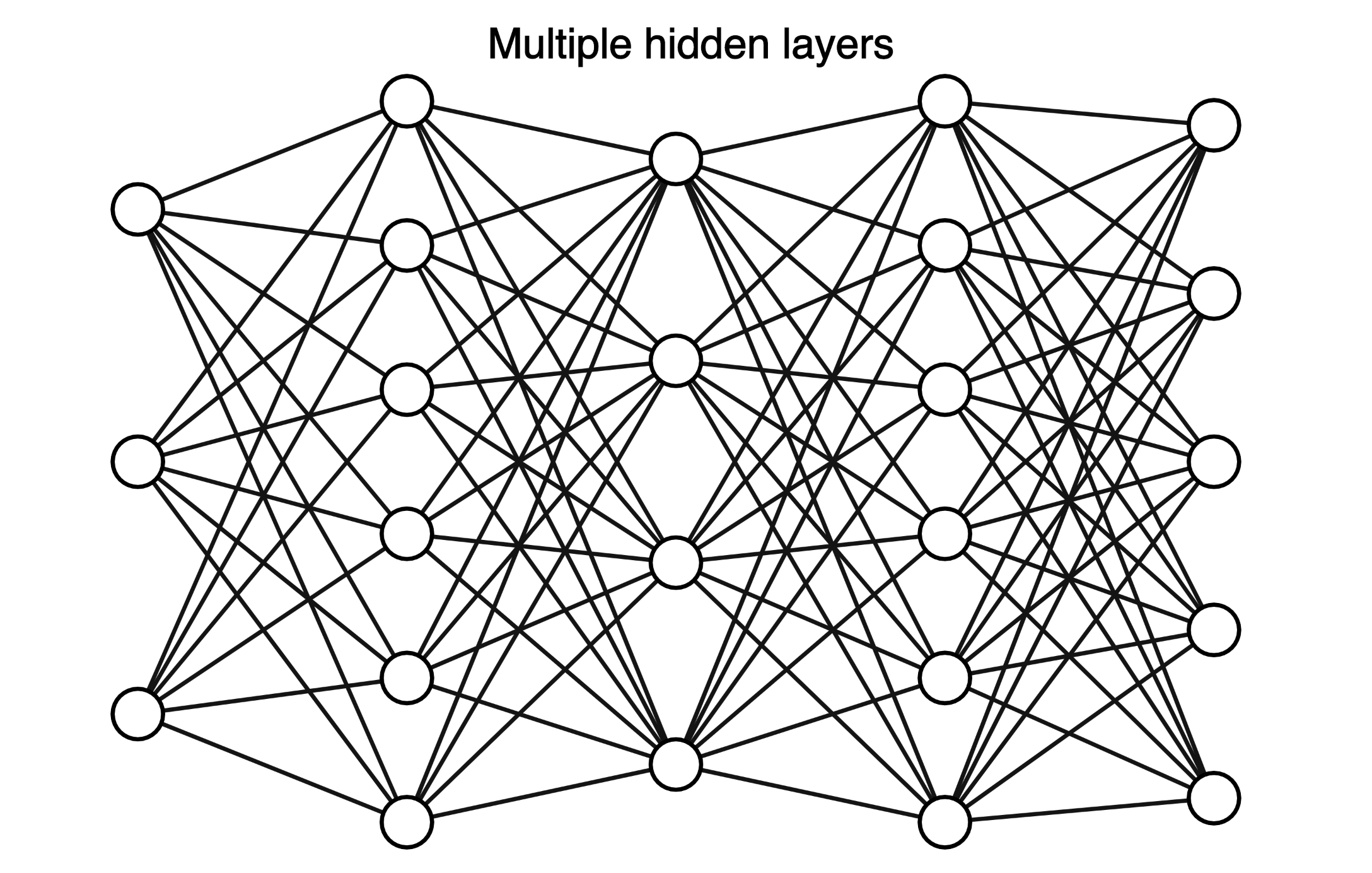
层级化的特征表示

机器如何学习:前馈

机器如何学习:误差的向后传递
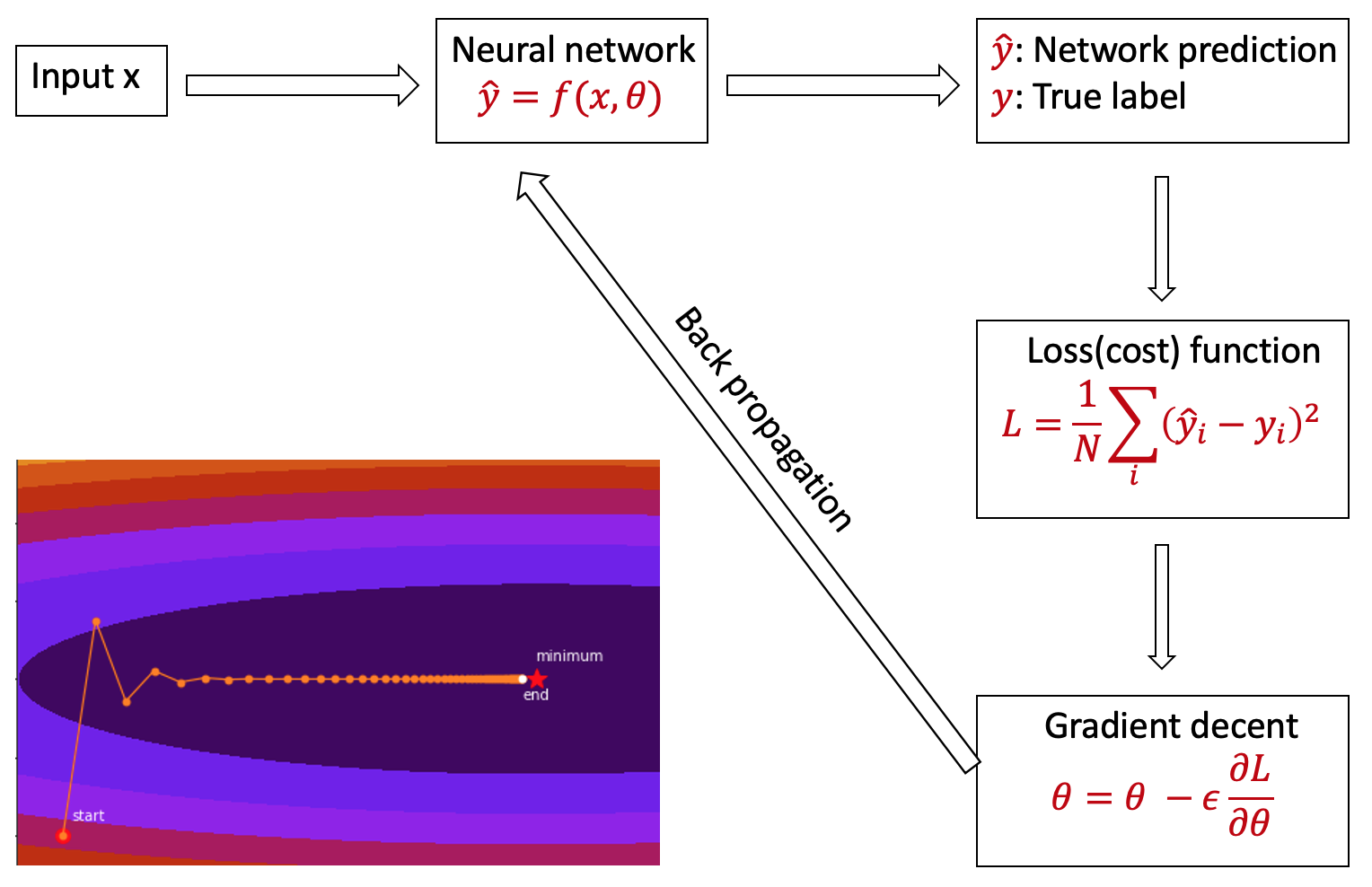
1 维梯度下降举例
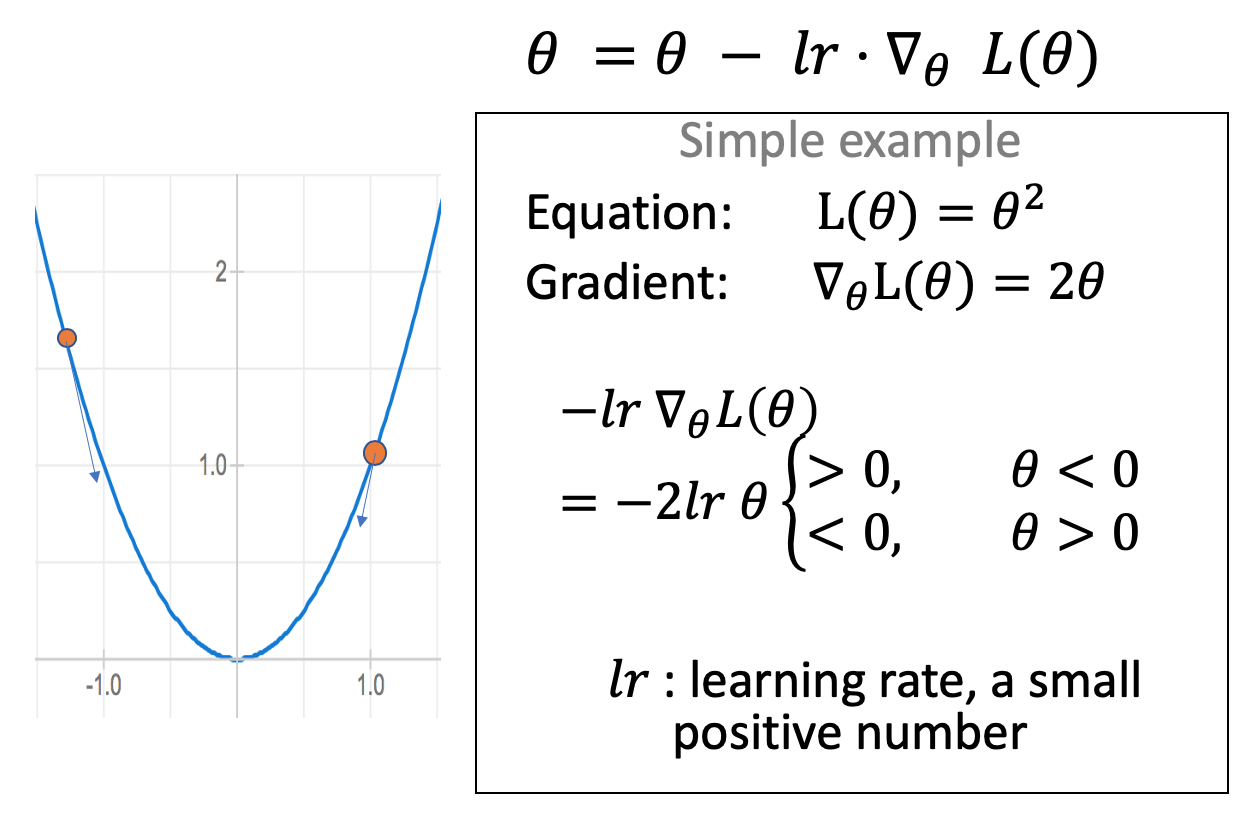
动量机制:越过局域极小值点
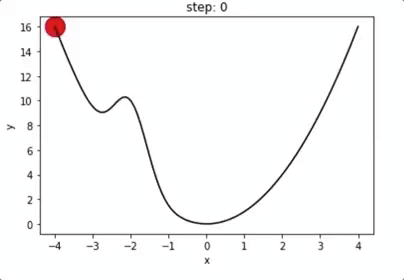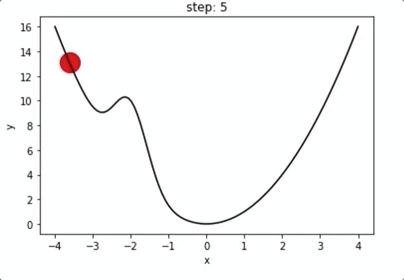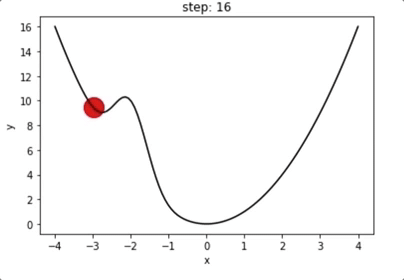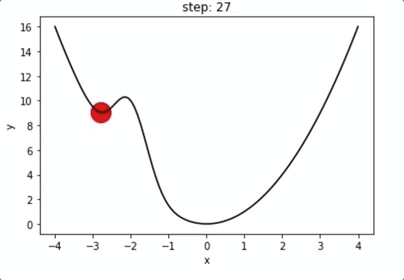
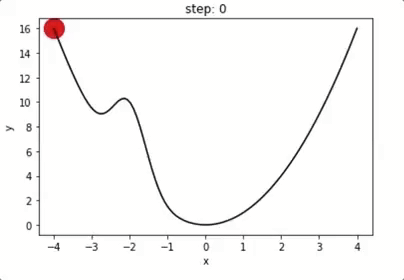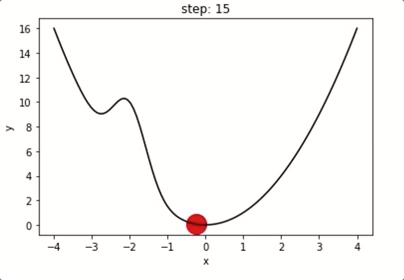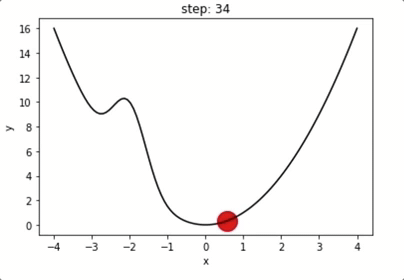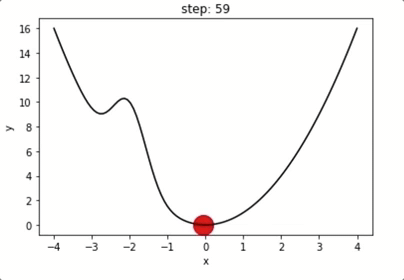
局域极小值?
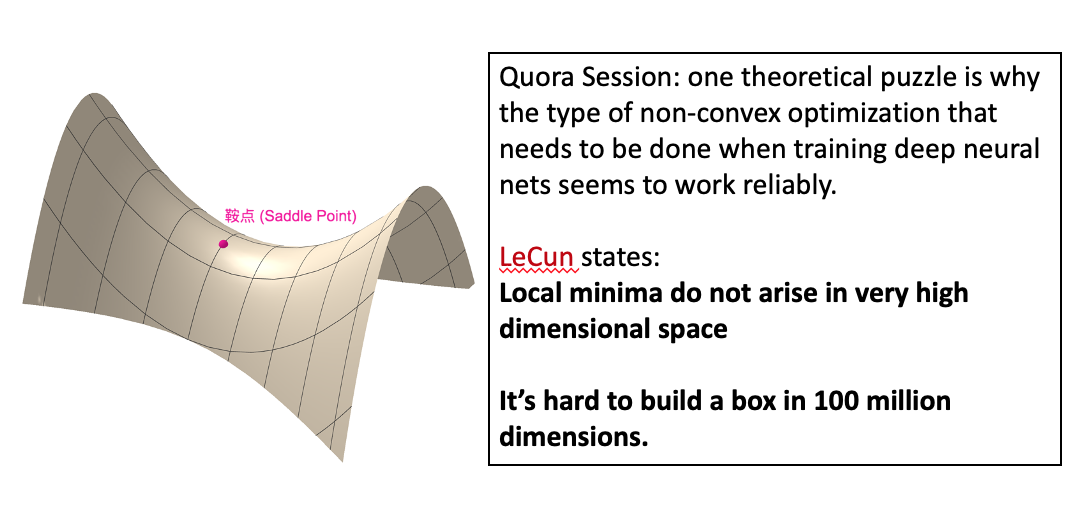
\(P(极小值)= 0.5^n \sim 0\) 其中 n 是神经网络参数个数。
深度神经网络为何不过拟合?
冯.诺伊曼: 使用4个参数我可以拟合一头大象, 再多一个参数,我可以让它的鼻子摇起来
- 深度神经网络参数众多,但需要拟合的数据更复杂
- 局域极小值存在的几率远小于鞍点存在概率
- SGD中的随机扰动与动量机制可跳出鞍点与局部极小值
- 众多正则化方案,及减少神经网络参数的办法
避免过拟合的方法
- Early stopping
- Train, validation, testing
- L1, L2 Regularization, weight decay …
- More data
- accumulate more training data
- data augmentation (crop, scale, rotate …)
- Fewer parameters
- Dropout, Drop connection
- Go deep. S.Liang & R.Srikant, arXiv:1610.04161
- Convolution neural network
2 维卷积
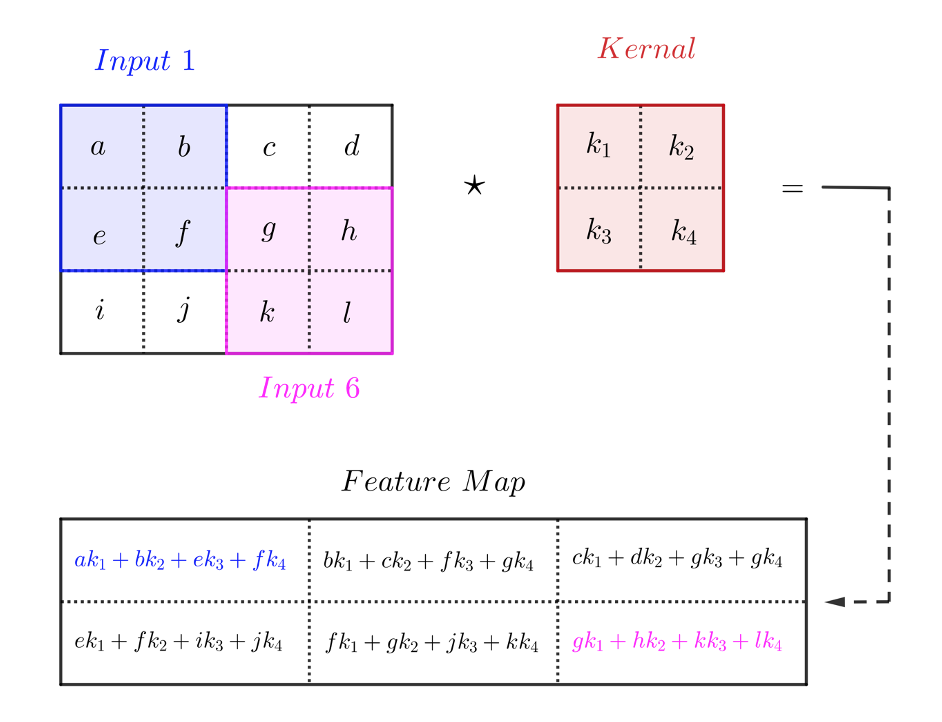
卷积的多输入通道
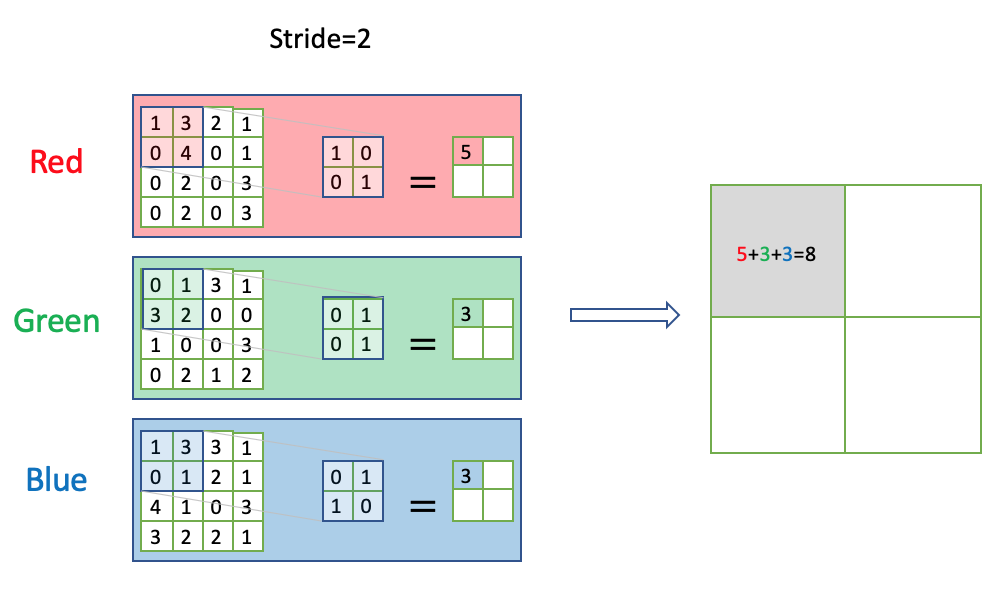
卷积的多输入通道
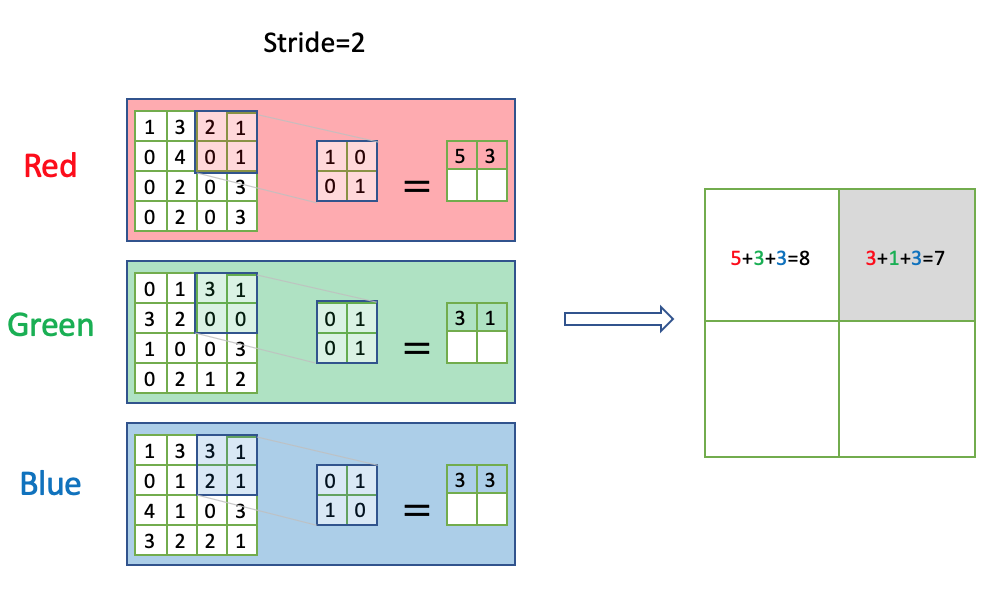
卷积的多输入通道
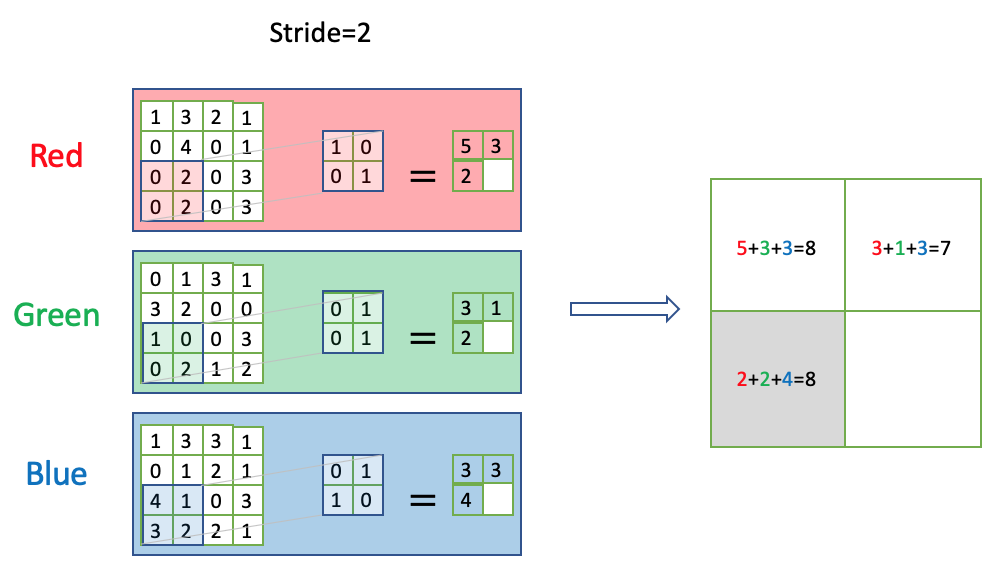
卷积的多输入通道
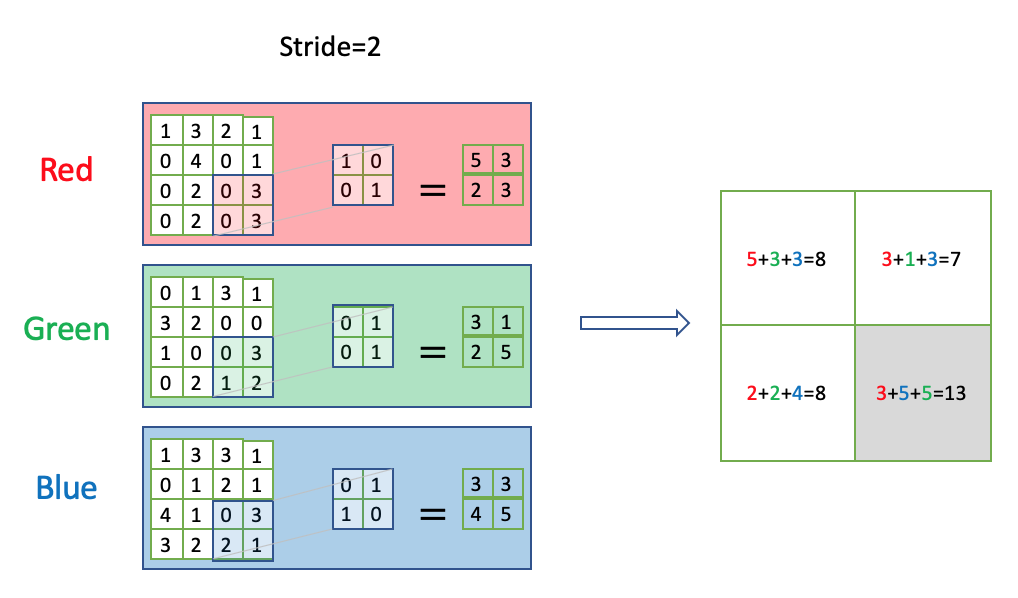
神经网络架构发展
卷积的多输出通道(AlexNet)
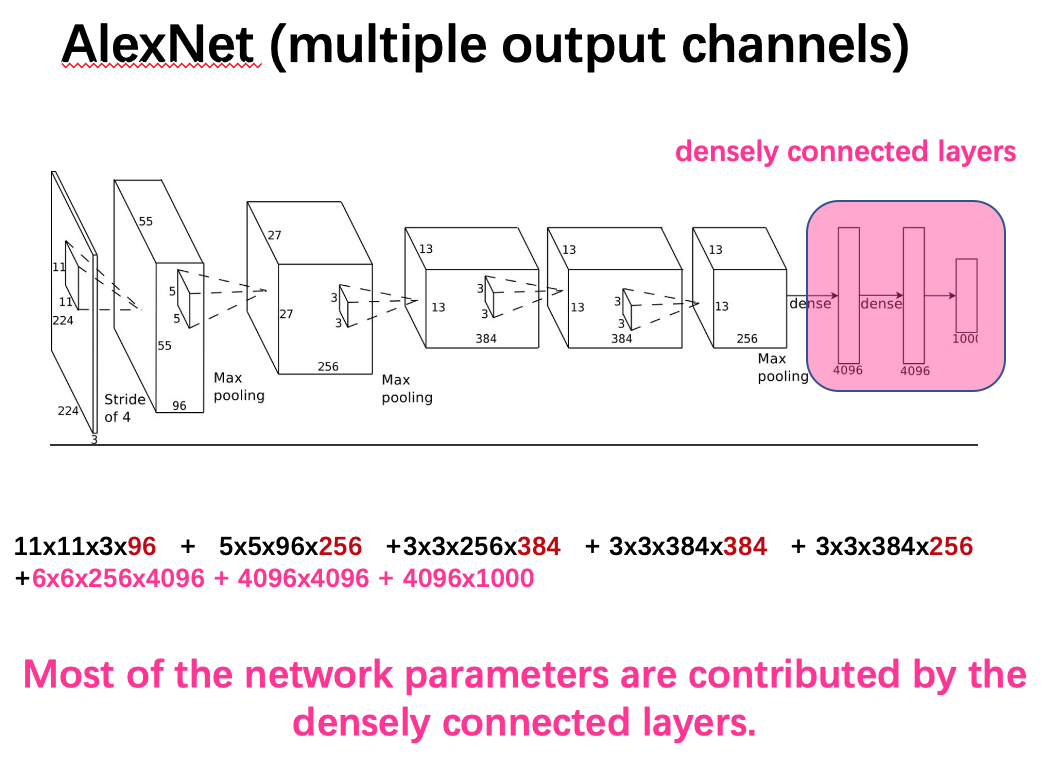
Global Average Pooling
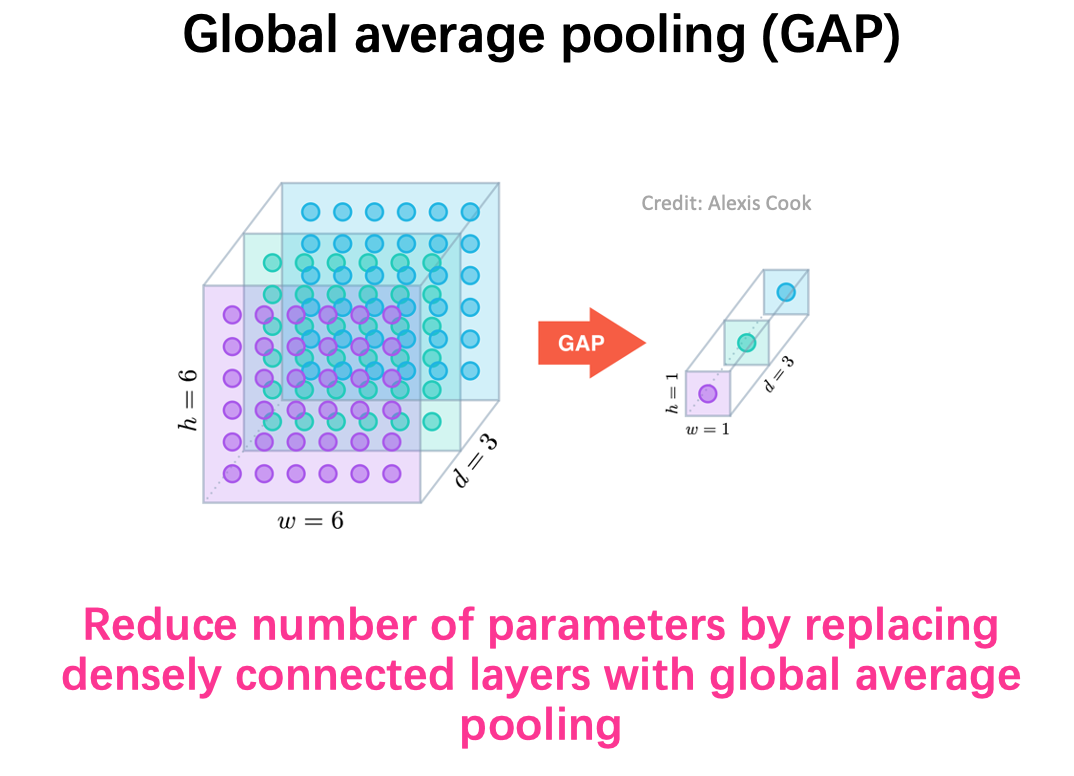
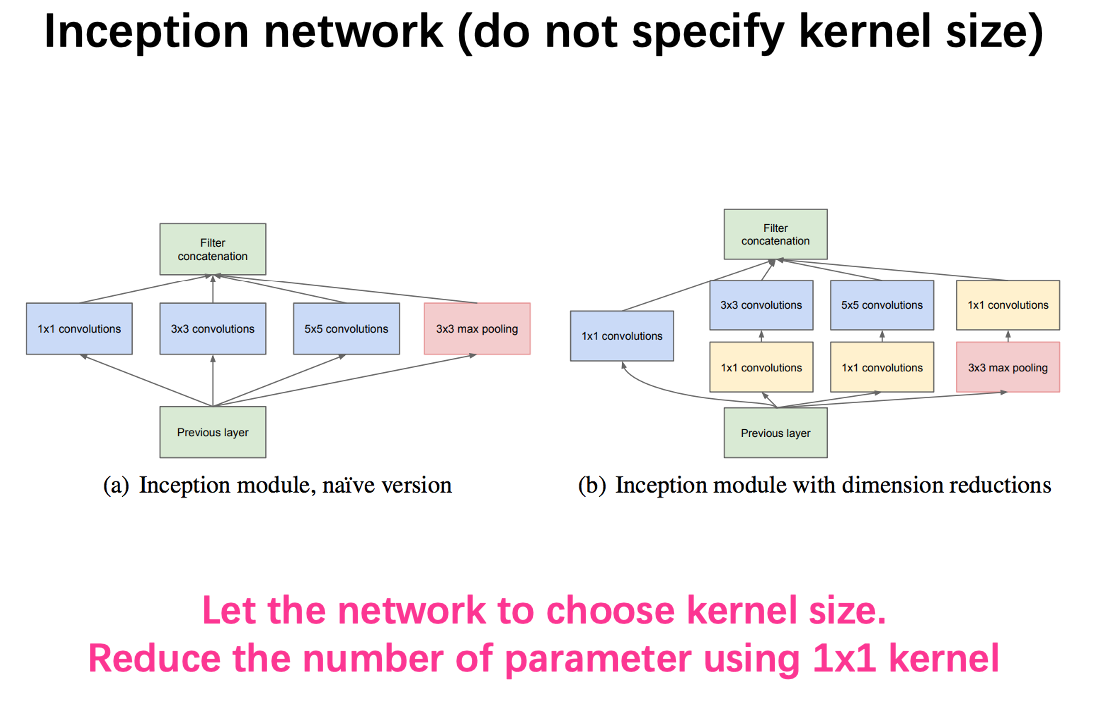
Inception Net
Residual Net

Squeeze Excitation Network

新学习理念
小数据上迁移学习 Fine Tune
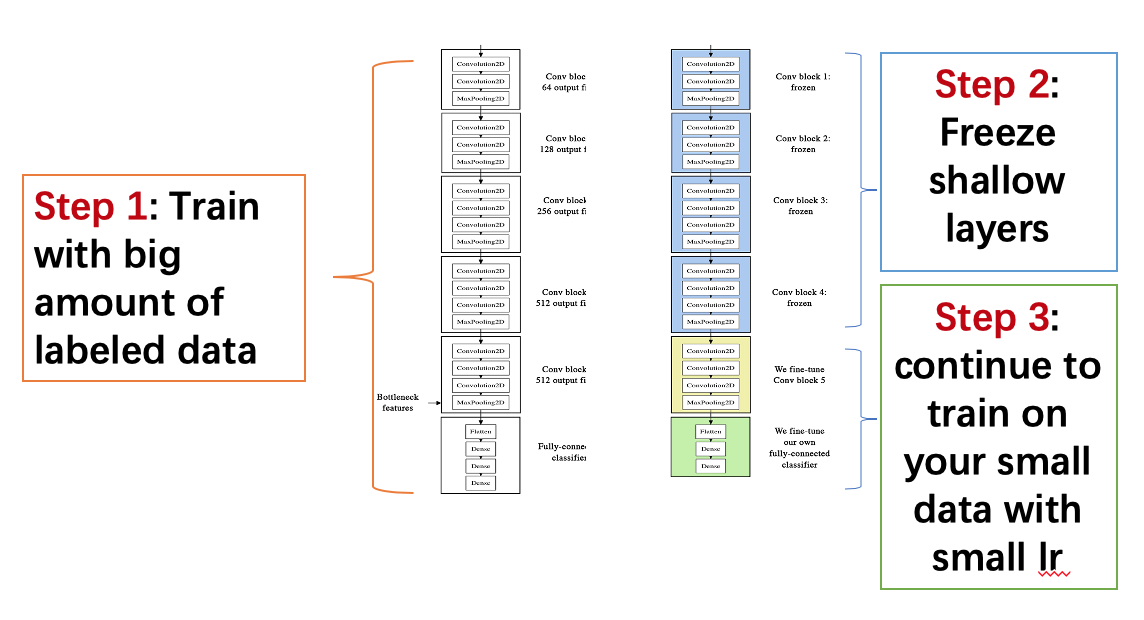
半监督学习

自监督学习

对比学习 (MoCo)
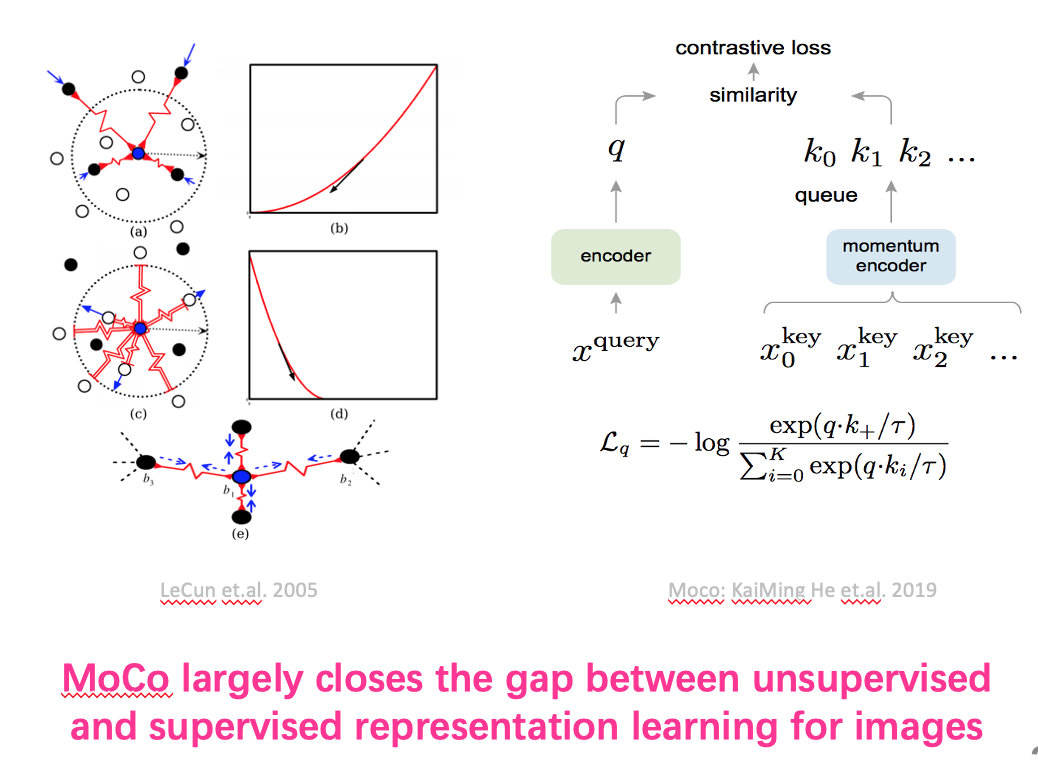
黑盒深度学习的可解释性
全局解释

梯度上升法,最大激活某个神经元
局部解释(替换法)

局部替换法,LIME或Prediction Difference Analysis
M. Tulio Ribeiro, et. al. “Why should I trust you?”
局部解释(类激活地图)

将深层卷积映射回输入图片
BoLei Zhou, et. al. “Learning Deep Features for discriminative localization”, CVPR 2016
局部解释(积分梯度法)
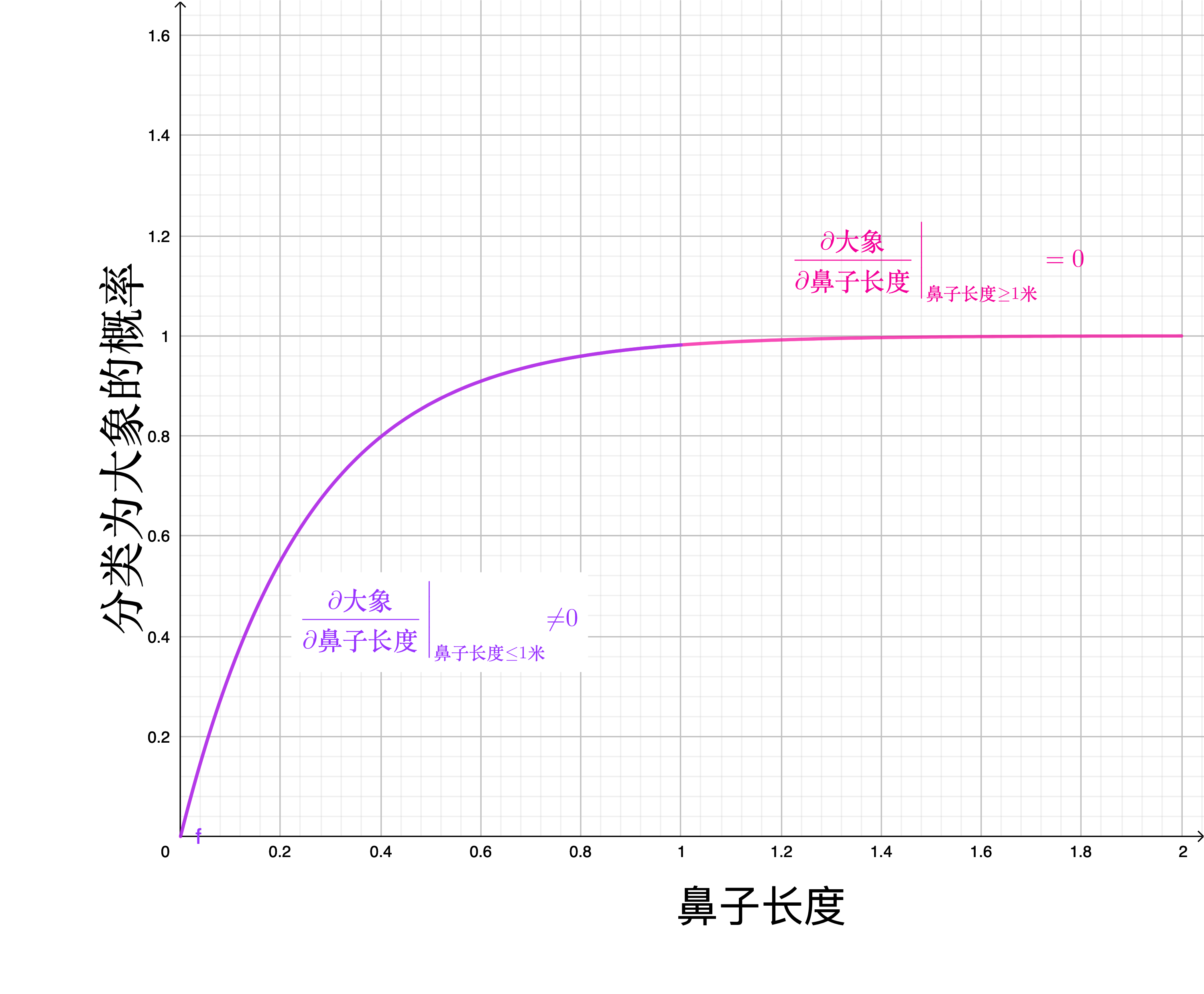
\(特征重要性 = \int_{0米}^{2米} \frac{\partial 大象}{\partial 鼻子长度} \quad\ d 鼻子长度\)
局部解释法(层间相关性传递)
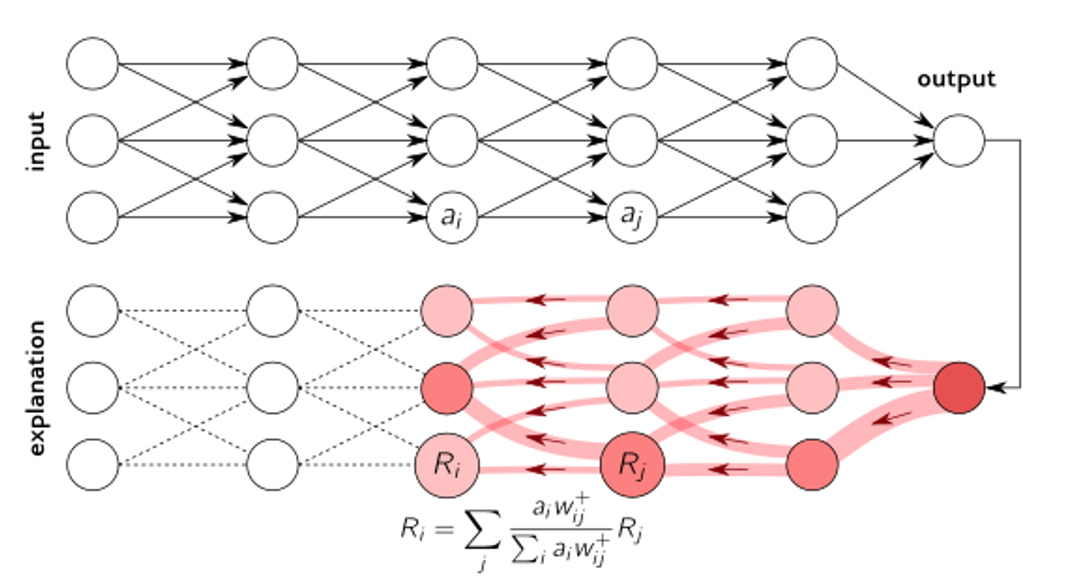
深度学习的不确定性
贝叶斯神经网络
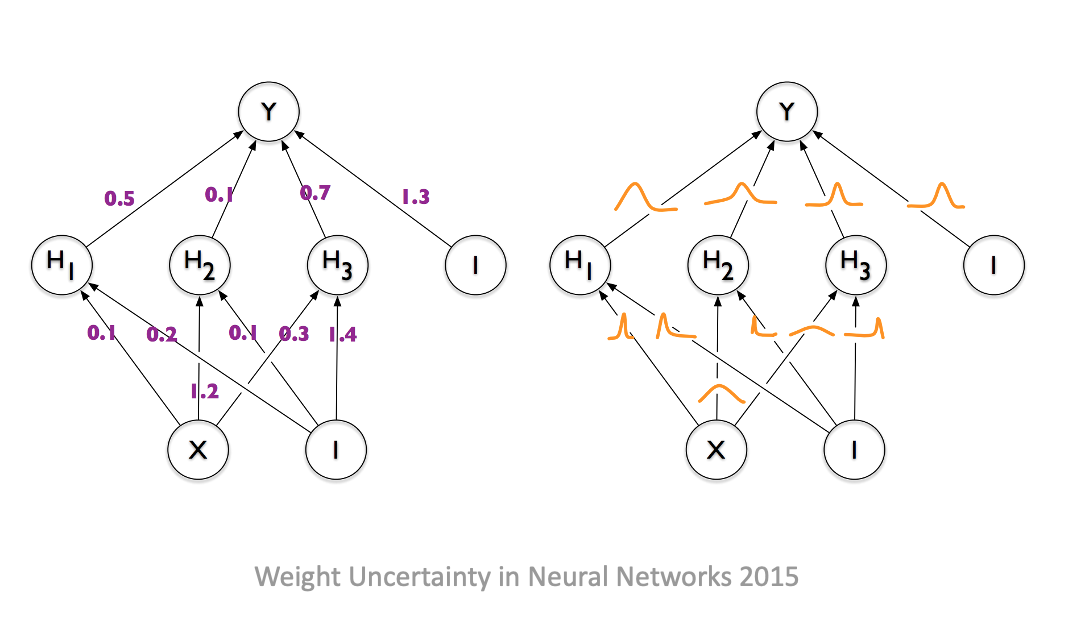
两倍的参数实现无穷多神经网络的系综。
蒙特卡洛 Dropout
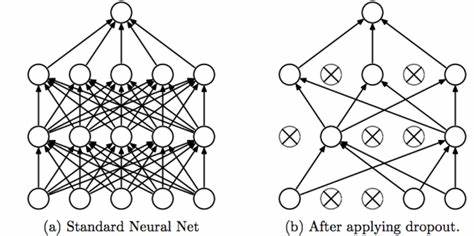
测试阶段打开Dropout, 生成神经网络系综
人工智能伦理
不作恶: 尊重隐私与公平
作恶的定义:己所不欲,勿施于人
- 智能监控学生
- DeepFakes 视频换脸
- 大数据杀熟
健壮: 免疫对抗样本攻击
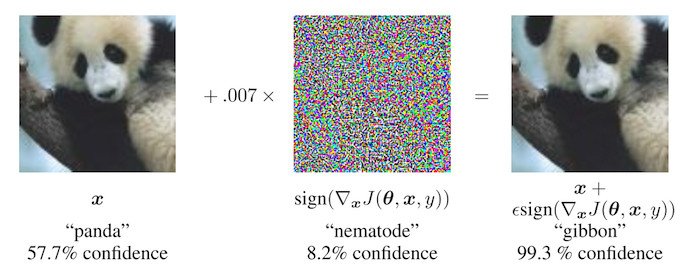
- 脆弱的模型眼中:熊猫 + 噪点 = 长臂猿
- 健壮的模型需要针对对抗样本训练
无偏见: 对训练数据进行无偏化处理

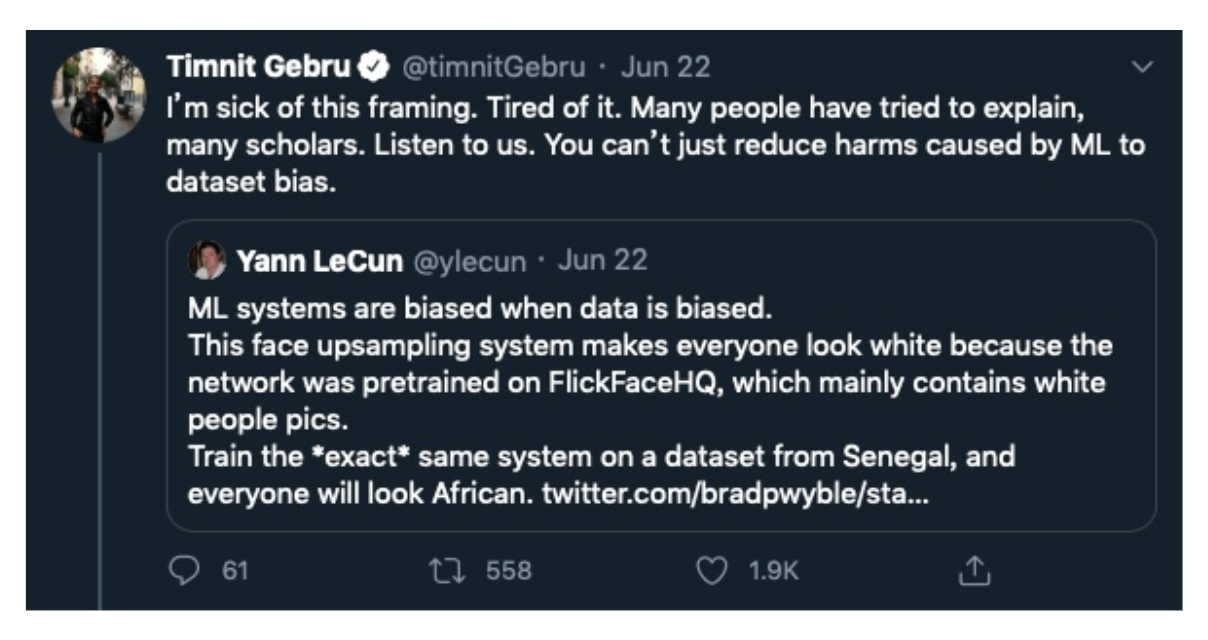
Duke大学开发的超分辨率程序 PULSE, 存在将低分辨率奥巴马照片恢复成白人的偏见。 Yann LeCun 因其个人言论被骂退出 Twitter。
学习资源
深度学习库 (Python is all you need)
- 百度:PaddlePaddle
- 华为:MindSpore
- 清华:Jittor
- 旷视:MegEngine
世界知名深度学习机构举例
书籍与视频
深度学习在反问题中的应用
《冯康传》中举例说明什么是物理学中的反问题。比如,
- “盲人听鼓”,盲人能否根据声音,判断鼓的形状
- “西瓜判熟”,敲击西瓜,通过声音判断西瓜是否成熟
- “油井勘探”,如何通过地震波,绘制地下油田结构
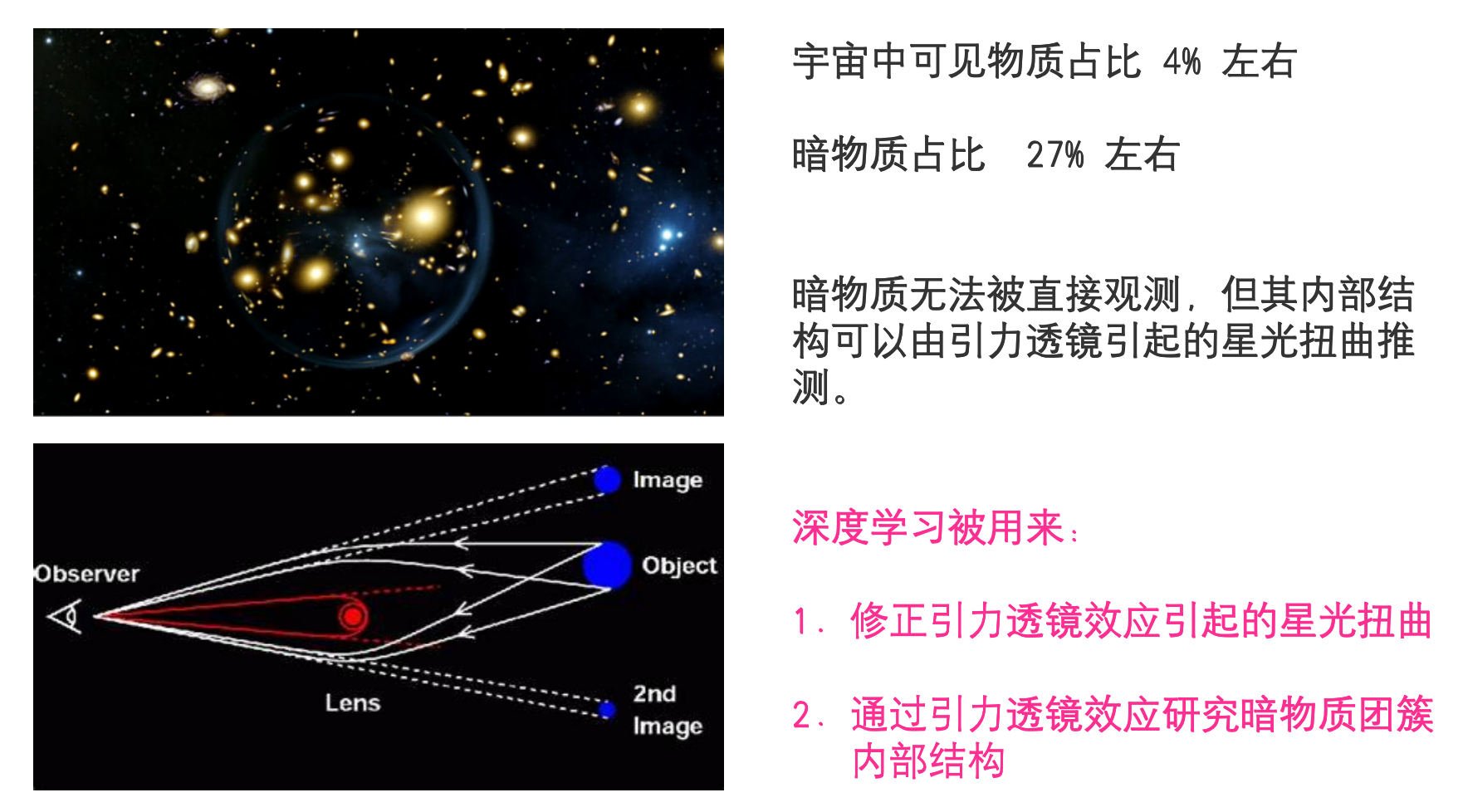
天体物理中反问题
高能核物理中反问题

- QGP 寿命\(\sim 10^{-23}\) 秒,无法直接探测
- 反问题(1)通过高能部分子穿过QGP时能损,反推QGP性质
- 反问题(2)通过 QGP 冷却后的强子分布,反推QGP性质
QCD 状态方程与临界点
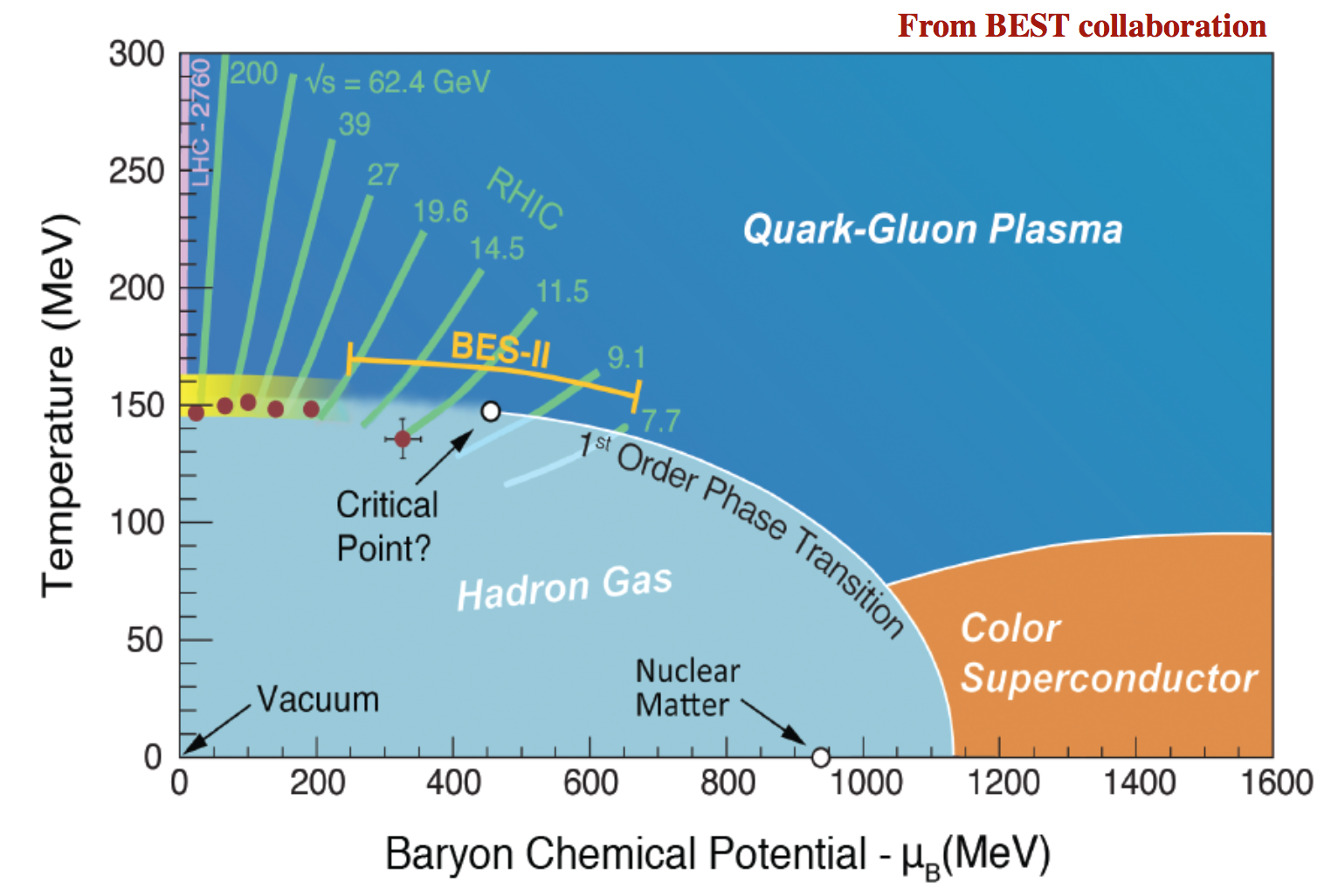
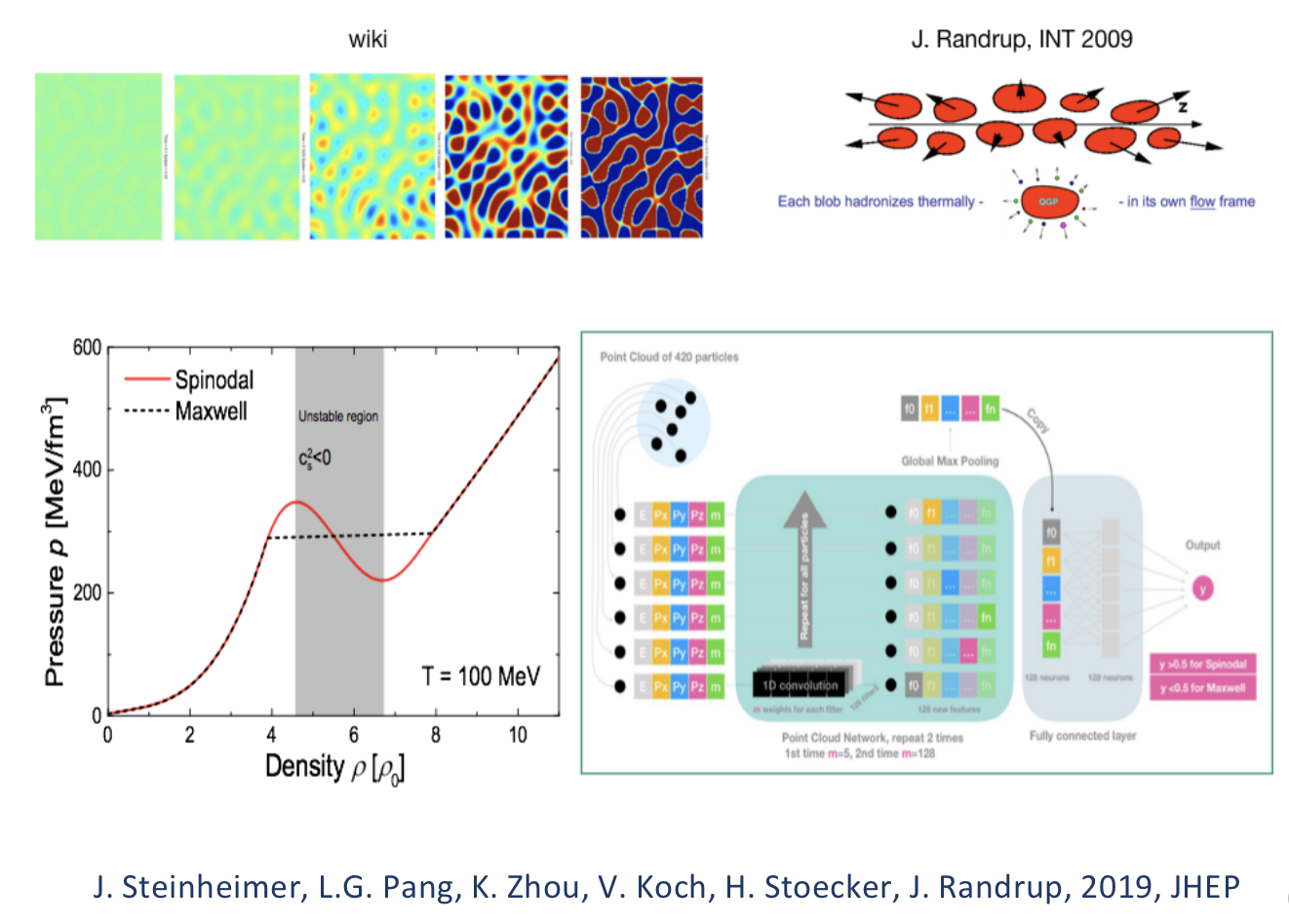
将临界点的寻找转化为相变分类问题
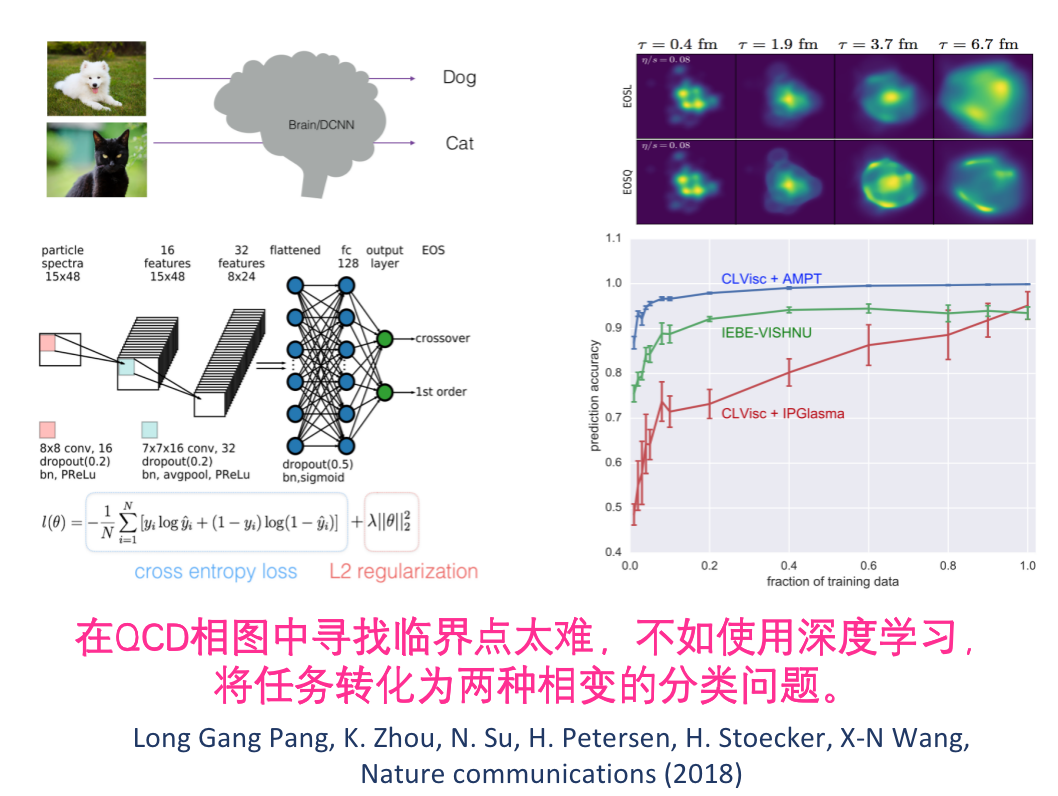
Maxwell and Spinodal 相变分类
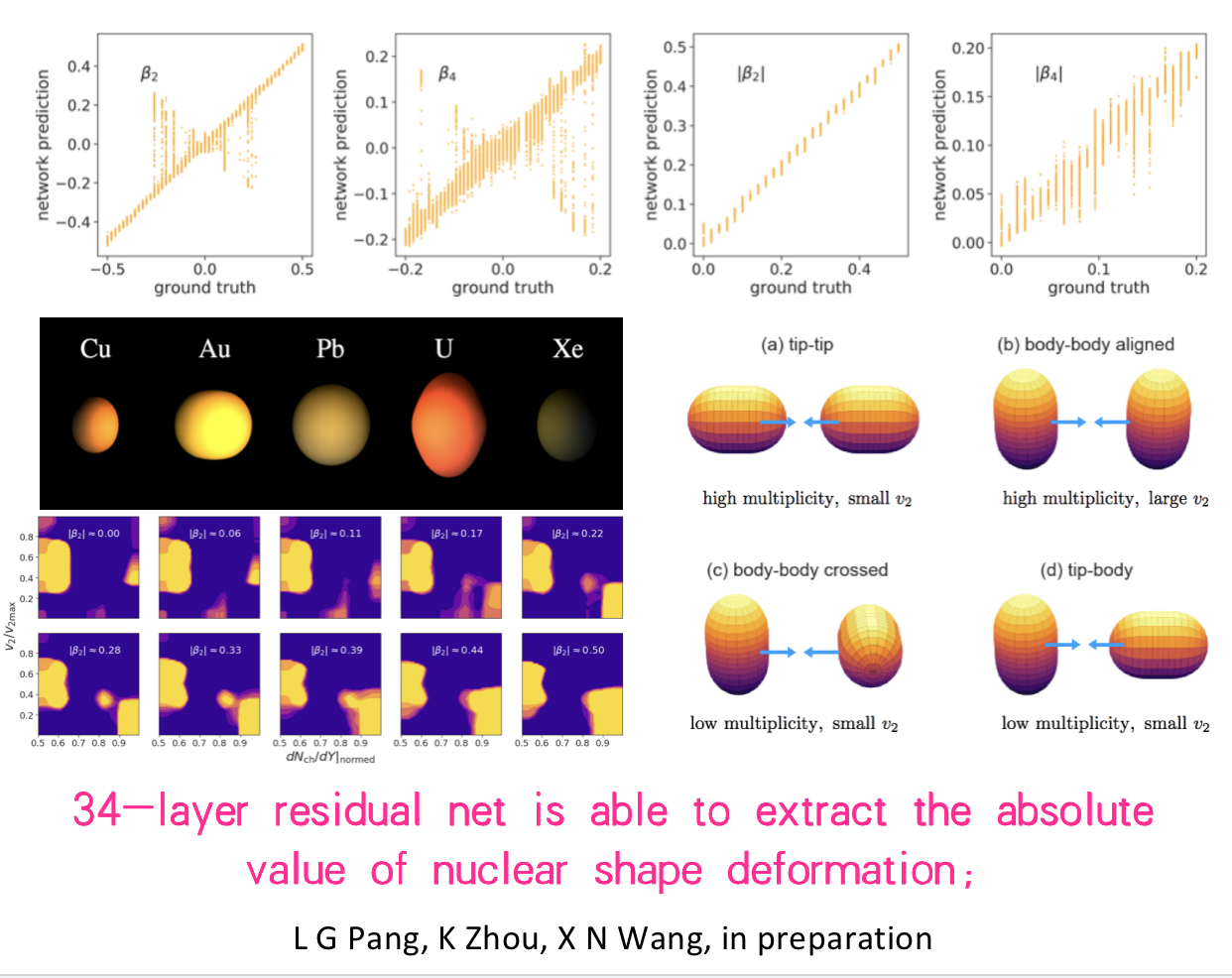
通过相对论重离子碰撞确定核变形
物理中的变分问题
求解偏微分方程:使用神经网络近似偏微分方程的解,优化解对方程,初始条件,边界条件的破坏
使用实验观测确定偏微分方程系数, 流体力学输运系数或哈密顿量
使用神经网络替换物理模型中无解析解或无数值解的模块。例如,无人机的近地湍流; 机器人反问题中关节摩擦力, 质量分布的建模
用神经网络表示偏微分方程的变分解

确定偏微分方程系数
参数未知的 Burgers 方程
\(u_{t}+\lambda_{1} u u_{x}-\lambda_{2} u_{x x}=0\)
Physics Informed Neural Network 近似:
\[f := u_{t}+\lambda_{1} u u_{x}-\lambda_{2} u_{x x}\]
最小化损失函数:
\[ L= \frac{1}{N} \sum_{i=1}^{N}\left|u\left(t_{u}^{i}, x_{u}^{i}\right)-u^{i}\right|^{2} + \frac{1}{N} \sum_{i=1}^{N}\left|f\left(t_{u}^{i}, x_{u}^{i}\right)\right|^{2}\]
使用神经网络的自动微分与梯度下降,学习物理规律。
变分蒙特卡洛:RBM for ISing 变分波函数
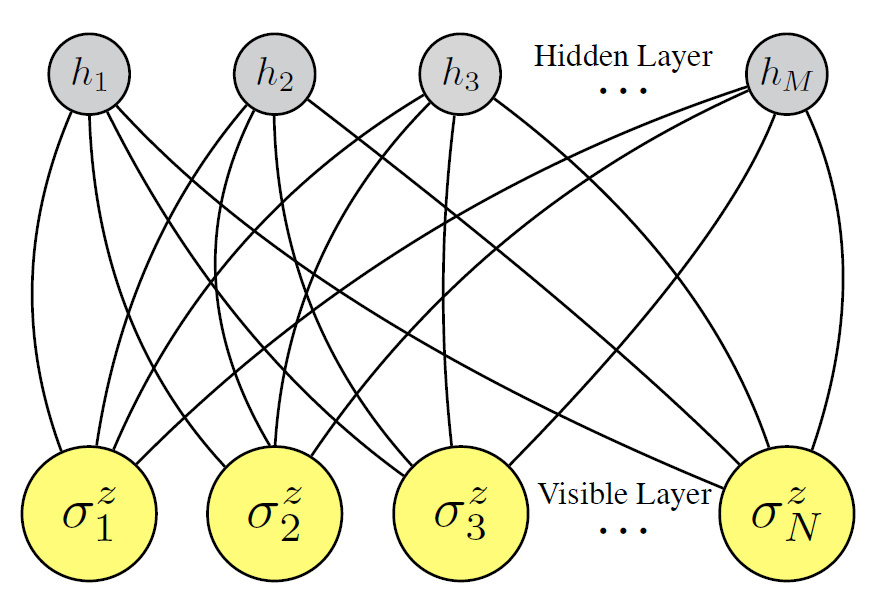
\[E_{\theta}=\frac{\left\langle\Psi_{\theta}|H| \Psi_{\theta}\right\rangle}{\left\langle\Psi_{\theta} \mid \Psi_{\theta}\right\rangle}\]
物理中的生成问题
- 深度学习任务:分类,回归,生成
- 生成模型无监督学习训练数据的统计分布
- 受限玻尔兹曼机 RBM
- 变分自编码机 VAE
- 生成对抗网络 GAN
- 自回归模型 Auto Regressive
- 流模型 Flow Model
生成格点量子场论构型 (生成对抗网络)
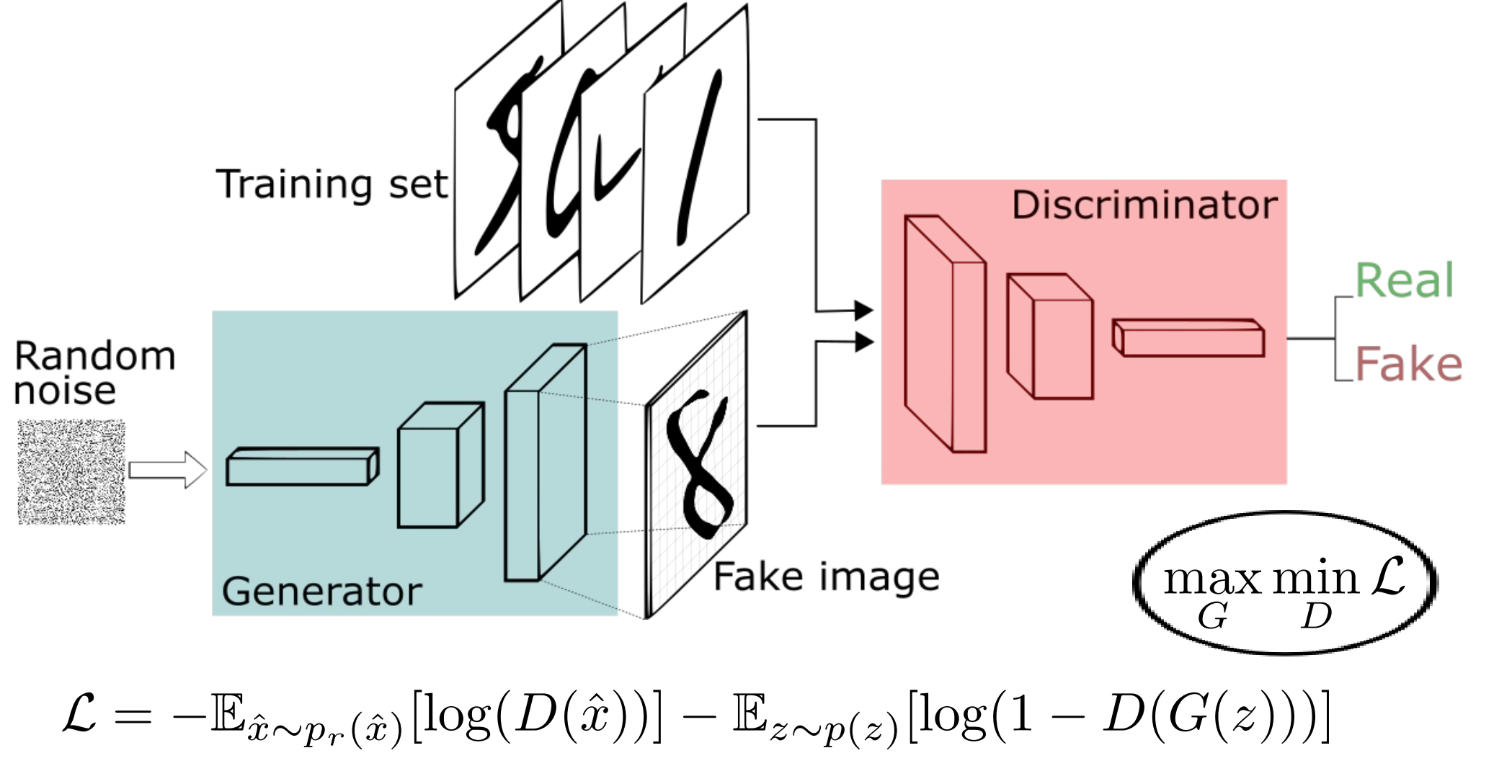
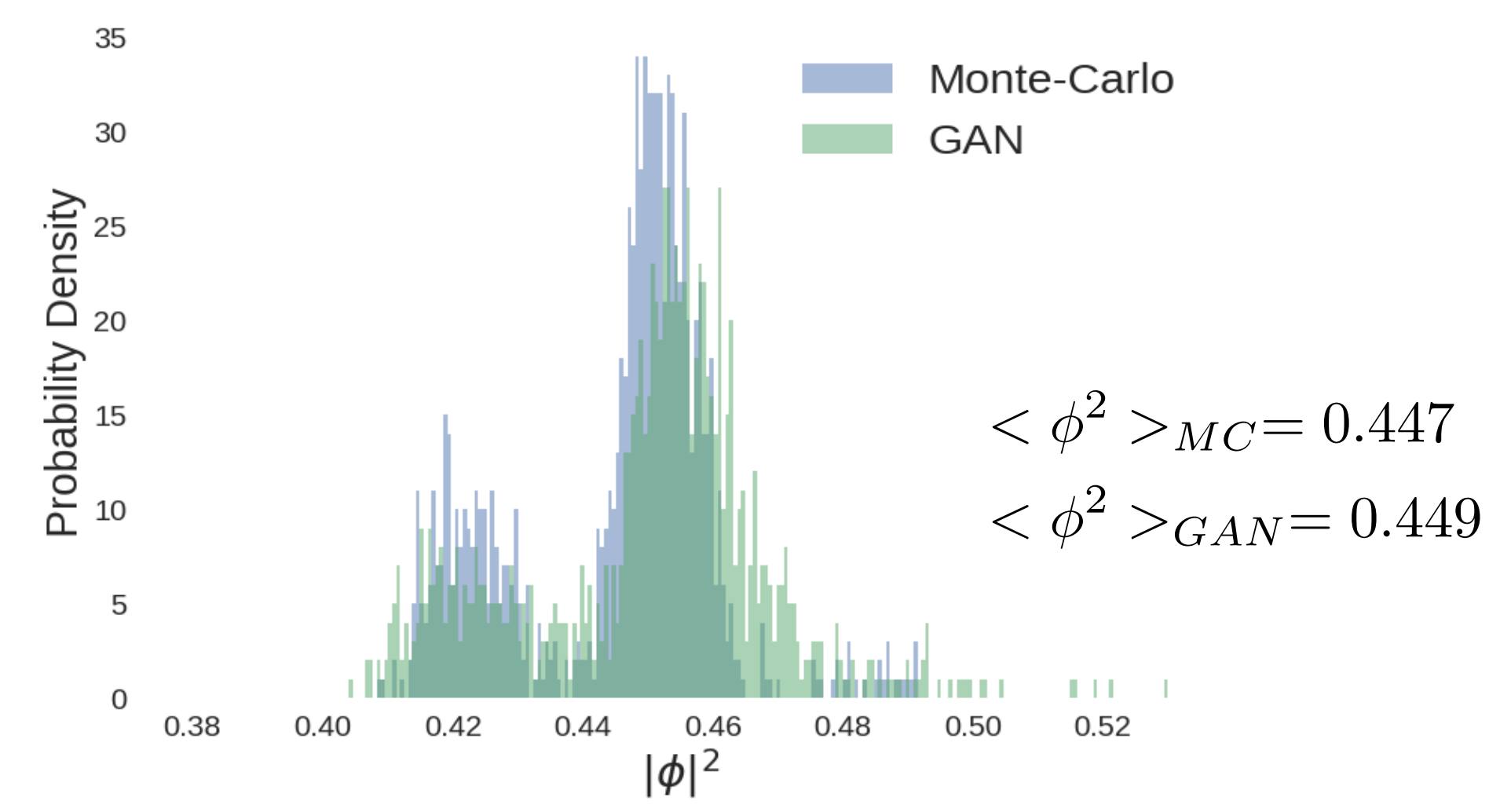
生成格点量子场论构型 (生成结果)
加速天体物理模拟
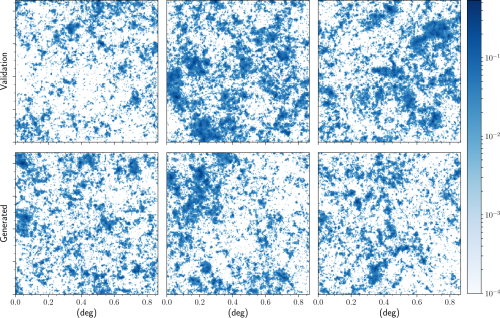
CosmoGAN: Training a Neural Network to Study Dark Matter
自回归模型解统计力学问题

![]()
\[P(z) = P(z_0) P(z_1 | z_0) P(z_2 | z_0 z_1) \cdots P(z_m | z_0 z_1 z_2 \cdots z_{m-1})\]
流模型: 双射,可逆的生成模型
在流模型中加入辛条件,实现特征解耦的抽样。
Neural Canonical Transformation with Symplectic Flows; ShuoHui Li, C.X. Dong, L.F. Zhang, L. Wang; PRX2020
物理学对深度学习的启发
重整化群解释
\[f(x) = \sigma(... \sigma(\sigma(x W + b) W + b) + b) \]
- CNN从浅到深逐层粗粒化特征提取
- 重整化群: 递归粗粒化得到给定尺度下最相关的物理特征
- 文章证明重整化群与深度信仰网络(多层受限玻尔兹曼机)存在精确映射
规范等变卷积

使用群论,构造平移和旋转等变的卷积
Spherical CNNs. Taco S. Cohen, Mario Geiger, Jonas Koehler, Max Welling. (ICLR), 2018
拉格朗日神经网络: 内嵌物理先验

使用神经网络构造正定的机器人质量矩阵 M(q)。
\[ L = T - V; \; T=\frac{1}{2} \dot{\mathbf{q}}^{T} \mathbf{M}(\mathbf{q}) \dot{\mathbf{q}}\] \[ \frac{d}{d t} \frac{\partial L}{\partial \dot{q_{i}}}-\frac{\partial L}{\partial q_{i}}=\mathbf{\tau}_{i} \]
\(\tau_i\) 是待预测的电机驱动力。
国内其他人工智能+核物理研究不完全列表
裂变碎片产额分布
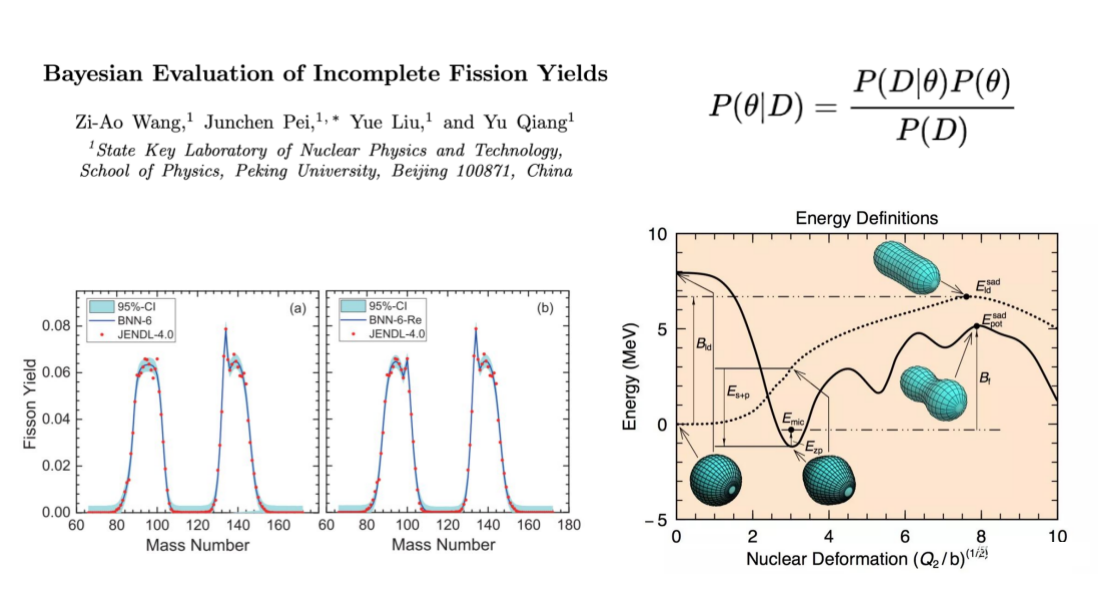
核质量与核裂变

相对论流体力学
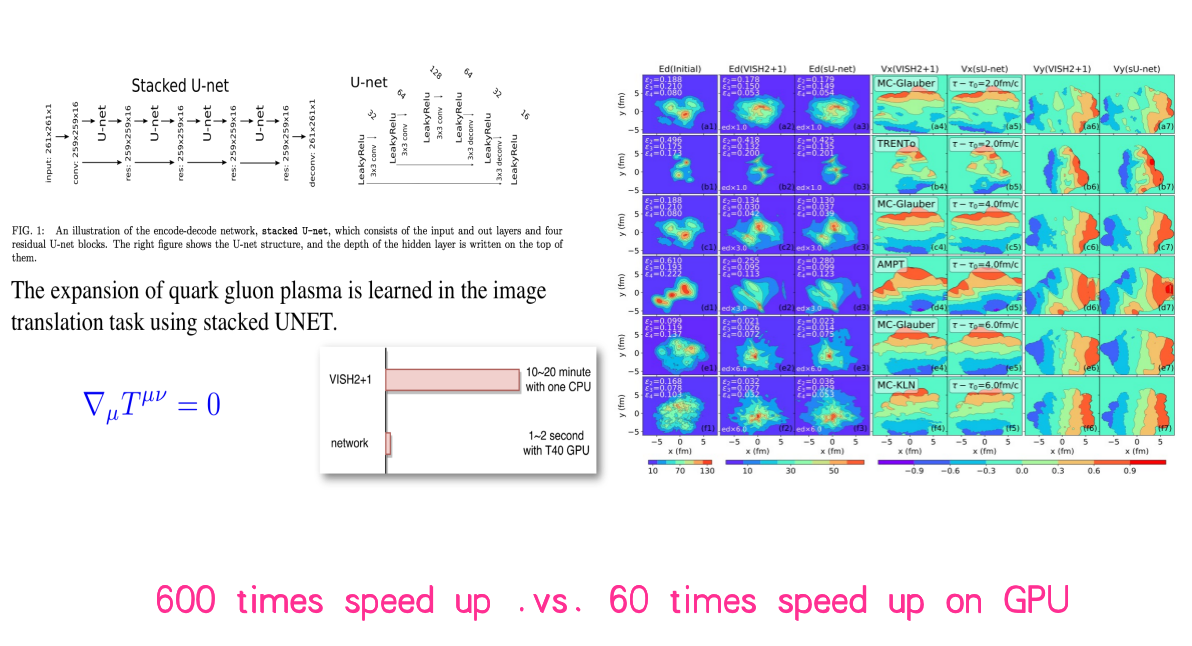
arXiv: 1801.03334; NPA2018, H.Huang, B.Xiao, H.Xiong, Z.Wu, Y. Mu and H.Song
总结
- 介绍了深度学习基本原理及研究方向
- 深度学习在物理学反问题,变分问题和生成问题中的应用
- 物理学在深度神经网络发展中提供的启发